| Home | AmMin | GMR | RiMG | Collectors Corner | Directory | Short Courses | |
|
|
|||||||

|
|
Volume 30, pages 469-482, 1945 THE GENESIS OF TWIN CRYSTALS M. J. BUERGER, Massachusetts Institute of Technology, Cambridge, Massachusetts ABSTRACT Interest has recently been indicated in a possible cause for the occurrence of twins. Apparently the only popular approach to twinning has been through the empirical rules of twinning enunciated by the French School. The writer's views, now some twenty years old, are herewith presented as a rational, structural approach to the cause of twinning. Since a stable crystal represents the least energy state of a collection of atoms, it is evident that the twin boundary must correspond with a higher energy state. It is shown that this higher energy is largely associated with the higher coordination spheres of the atoms. That a twin can form at all requires that the first coordination conditions of the atoms at the boundary are satisfied. This view is purely structural and has been substantiated in twins which have been considered with regard to structure. On the basis of genesis, twins may be divided into the categories of growth twins, transformation twins, and gliding twins. Growth twinning is caused by an accidental departure from equilibrium during growth, and is favored in the nuclear stage, especially under conditions of supersaturation. Transformation twinning is a consequence of high-low inversion. Glide twinning is caused by a specific type of structural shear in plastic deformation. Parting is, in part, a consequence of the high energy in the twin boundary. The act of twinning has analogies with the act of transforming from one polymorph to another: growth twinning corresponds with reconstructive transformation; glide twinning corresponds with displacive transformation. Transformation twinning is a special case of unmixing. The oft-repeated saying that twinning represents the result of an effort on the part of the crystal to assume a greater symmetry is the exact opposite of the true state of affairs. INTRODUCTION In recent papers1,2,3 some observations on the occurrence of twinning have been made and the question of what is responsible for the formation of twins has been raised. The writer's own views on this question have had a limited circulation. In view of the general interest in the subject, it seems desirable to give them wider publication. The cause of twinning is easily approached through energy considerations. A stable crystal represents the lowest free energy state of that collection of atoms; this follows from the very notion of stability. The pattern preferably assumed by atoms assembling themselves as a crystal is thus the configuration of least free energy. Any departure from this pattern represents an increase in the energy of the collection of atoms. Since the pattern of atoms in the twin boundary represents a departure from the rest of the crystal pattern, it is obvious at the outset that the twin boundary region is a locus of higher energy than the rest of the crystal. What permits these atoms to assume this configuration of higher energy? To answer this question is to assign a cause to twin formation. RELATION OF TWINS TO OTHER KINDS OF INTERGROWTHS The energy in the twin boundary is stored as surface or interfacial energy. This kind of energy also exists in the mutual boundaries of other kinds of intergrowths. The writer has pointed out4 that the locations of the interfaces of unmixing intergrowths is conditioned by requirements of minimum interfacial energy, and that low energy is made possible by the existence of a plane of atoms in common between the two unmixing phases. This provides a gradation in structure rather than a complete discontinuity; consequently the additional energy in the junction plane is not far above that of a plane in either crystal. This near-minimum energy requirement naturally occurs in all kinds of intergrowths and it conditions the mutual orientations of crystals in such intergrowths.5 Attention is now directed specifically to intergrowths of the same species of crystal. In the genesis of such intergrowths, assuming that the individuals of such pairs do not arise independently of one another, the most probable orientations are such as to provide the greatest number of structural elements in common. This structural relationship provides reduced interfacial energy. Other things being equal, the greater the number of atoms in the region of the interfacial plane which are able to participate normally in the bonding of the two structures, the less abrupt is the discontinuity, the lower is the energy, and consequently the more probable is the intergrowth. For example, a less probable intergrowth would be one in which one set of translation-equivalent atoms were normally bonded to both of the structures, but with the rest of the structure suffering a discontinuity at the boundary. The most probable intergrowths are those in which, all atoms of the structure in the region of the junction bridge the junction. The bonding picture of this type of intergrowth will be discussed shortly. A twin is generally recognized as being a rational, symmetrical intergrowth of two individual crystals of the same species. In a very broad way, any intergrowth of two individuals of the same species is symmetrical, in the sense that one individual is a repetition of the other by some geometrical operation. When the operation conforms to the requirements for a crystallographic operation, it has conformed to the requirement for an operation which transforms a net into itself; the intergrowth is then rational. Rational intergrowths naturally have higher probabilities than non-rational intergrowths. STRUCTURAL REQUIREMENTS FOR LOW ENERGY These considerations have been rather general, but they are easy to translate into a structural picture. Without being specific regarding the type of bonding or the kind of structure, it can be said that the energy of an atom is a sum of a series of terms each representing the energy of that atom with respect to another atom in the configuration, the summation being carried out to all atoms in the configuration. Energy, in general, decreases very rapidly with distance; consequently the energy summation converges rapidly with distance. The nearest neighbors, therefore, are the highest contributors to the summation. Thus the first coordination sphere of an atom determines a large part of its energy, the second coordination sphere modifies this sum somewhat, and higher coordination spheres modify the energy sum to a lesser and lesser extent. Evidently an atom can participate in a twin boundary structure and contribute a low energy to the summation provided it can merely satisfy its immediate coordination requirements. In the comparatively few cases in which the attention has been called to the relation between a structure and the transition structure inferred for the twin boundary, 6,7,8,9,10 It has been evident that the twin exists by virtue of the fact that the atoms in the structure permit more than one linking of themselves consistent with their immediate coordination requirements, giving rise to two different configurations; one of these configurations represents the structure and its continuation, the other represents a transition to the twin configuration.It must be inferred from this that the existence of a twin is permitted by the nature of the structure itself. If the structure is of such a nature that, in detail, it permits a continuation of itself in alternative twin junction configuration without involving violation of the immediate coordination requirements of its atoms, the junction has low energy and the twin is energetically possible. This theory of the energy permissivity of twins emphasizes the characteristics of the structure itself, in contrast with the French theory of twinning, 1,3,11 which, ignoring the structure itself, merely requires certain special dimensional qualities in the identity periods of the structure. Furthermore, the French theory of twinning is strictly empirical, while the theory presented here is a rational one. Apparently the two theories are in conflict, but some relations between them will be considered further on in this paper.TWIN FORMATION INTRODUCTION There appear to be at least three distinct devices which are responsible for bringing about the high energy states of twin boundaries. Corresponding with these there may be recognized several genetic types of twins: growth twins, transformation twins, and gliding twins. In the following sections, some aspects of the genesis of these twins are considered. GROWTH TWINS Geometrical aspects. - To understand how twins develop during the growth of the crystal, one must be acquainted with the mechanism of crystal growth, for twins develop as accidents of the growth process. The general rule of crystal growth is that the newly arriving atom (or cluster of atoms) takes up a position such that the part of its normal coordination which it assumes on contact with the surface is a maximum as compared with what it would be on other parts of the surface. Thus, if the atom is the first one to arrive at a plane surface, all positions where it could continue the pattern are the same, and it can therefore assume any one of these identical positions. On the other hand, the next atom to arrive which can also coordinate with the first atom must necessarily assume a position so that it does coordinate with it; in this way, the atom improves its coordination and so loses more energy than by occupying a position on the plane and away from the first atom. In a like manner, each newly arriving atom locates itself in a place touching one or more of the atoms already located on the old surface, and the process of crystal growth consists of spreading of the new layer to cover the old surface. Under near-equilibrium conditions, a second new layer does not start to form until the first new layer is completed. During the process and until a layer is completed, there is always a corner at the base of the new surface to which atoms or clusters of atoms are especially attracted because of the greatest energy loss in the form of greatest coordination offered there. The above considerations are primarily concerned with the addition of atoms to the continuation of the normal pattern of the crystal. An atom can also fall into a position which does not continue the pattern, yet which satisfies its first coordination sphere. Should the atom fall into such a position, its energy would be an approximation to minimum energy, according to the discussion under "Structural Requirements for Low Energy." Since it does not have actually the lowest energy, however, it has a comparatively high fugacity, and it normally would lose its place for a more suitable one by a mechanism of thermal agitation and atomic bombardment. What factors are responsible for maintaining an atom in a position of subminimum energy? A possible factor might be the simultaneous arrival at neighboring positions of a pair of atoms or more which can mutually coordinate, or, what amounts to substantially the same thing, the arrival in the twin position of a group or cluster of atoms already coordinated. The entire cluster has a smaller fugacity than a single atom, and an atom bound within the cluster by coordination also has a lower fugacity than any single atom arriving alone at a subminimum energy location. If the arrival of the cluster at the subminimum location is immediately followed by the arrival of other atoms or clusters to continue the twin pattern, a twin may persist. We now turn to the empirical rules of twinning of the French School. Bravais 12 and Mallard13 observed that twins appear to be possible if the lattice of a crystal has a higher dimensional symmetry or pseudo symmetry than the crystal. These additional symmetry elements are the ones which relate the individuals of the twin and constitute the elements of the twin law. Friedel11 generalized this purely empirical rule and held that twins are possible even if a multiple cell (of small multiplicity) has a pseudo symmetry beyond the symmetry of the crystal. The occurrence of twinning, according to Friedel, is more probable the lower the "index" (which is related to the multiplicity) of the pseudo cell and the smaller the obliquity of the row in this cell to an ideally symmetrical row.
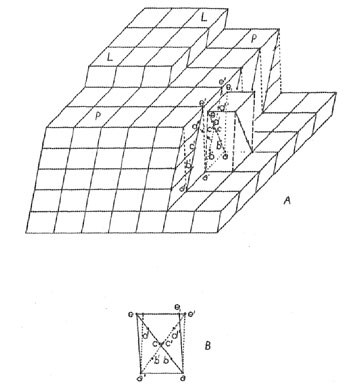
It should be possible to interpret the findings of the empirical French School on grounds of energy and with the aid of the theory of crystal growth by spreading of one layer over another. A stage in the normal growth of the crystal is represented in Fig. 1A. Here the representation of the crystal is by means of cells in accordance with the French School, not by means of structure. The crystal plane, PP, which is growing, is being covered by the new layer, LL. The cliff at the right shows how the simple cell is related to Friedel's dimensionally more symmetrical multiple cell. Now if, at any time, such a cliff is momentarily established, say, due to rapid growth, it becomes geometrically possible for several atoms (or a cluster) to add themselves to both surfaces of the reentrant at the foot of the cliff. The two surfaces of the reentrant provide a greater-than-normal coordination for a large cluster, especially as compared with the plane PP alone. Thus, should a cluster arrive in twin position, it might be able to retain this subminimum energy attachment merely because it has a multiple grip on the crystal which acts as a considerable energy barrier to removal. Once established, the pattern of the twin continues. If this view is correct, then the interpretation of Friedel's rules must be as follows: the geometry of the lattice aids twin formation because a cluster, represented by points abcde, Figs. 1A and 1B, arriving at the crystal, can superpose itself in twinned orientation on the untwinned. crystal, a'b'c'd'e', since a small cluster is sufficiently elastic. Thus e1 coincides with e' and c with c'. Friedel's angle of obliquity is then half the three-dimensional angle e'ael. Such strain is directly proportional to the tangent of the angle. (A continued coincidence of the two twinned parts of the crystal is unlikely since it involves the work of shearing the entire crystal through the angle of obliquity.) The significance of Friedel's low multiplicity of the multiple cell would be that as many points as possible, such as e and c, should be capable of joining the crystal and its twinned structure. At this point it is necessary to amend the French theory.* Its rules provide, perhaps, necessary conditions for certain growth twins to occur, but they are definitely not sufficient conditions. The French theory, as it stands, provides only an incomplete picture of permissivity of twinning. To amend it we add the requirement of low energy junctions from twinned to untwinned structure, at least at the point of inception of the twin. This implies, in general, that the structure must be continuous, at least in the nearer coordination spheres of the atoms in the junction structures. It should be emphasized that this requirement is not only rational, but it has been found to hold in such twins as have been examined with regard to structure. Environment factors favoring genesis of growth twins. - In addition to the geometrical factors permitting growth twinning, just discussed, certain external and internal environmental factors encourage the formation of structures of subminimum energy. Among these are supersaturation and minuteness of crystal. It is evident that if the rate of addition of atoms to the surface of a crystal is sufficiently high, the probability will be increased that an atom arriving at a twin position will not be relocated before it is joined by a second atom. Once a second atom joins the first, the pair has a very low energy because each member has its coordination increased by the other. Thus, once started, the twinned layer may persist and grow. The probability of twin formation increases with the rate of addition of atoms or clusters to the crystal, and thus, within limits at least, increases with the degree of supersaturation, suggesting the genetic name supersaturation twin. While supersaturation may cause twinning at any time during the history of growth of the crystal, the most obvious time when the degree of supersaturation is very high is just before nuclei start to form. Once nuclei appear, the immediate regions surrounding them become cleared of a high degree of supersaturation, and a normal growth rate is established consistent with the rate of diffusion. For this reason, the condition causing supersaturation twins is most likely to arise just once - as the crystal nucleus forms - and then the conditions leading to this type of twinning do not usually occur again. Nuclei supersaturation twins are therefore characteristically simple pairs (such as Carlsbad, Baveno, and Manebach twins in feldspars). This condition is enhanced by the factor discussed in the next paragraph. Supersaturation twins can, however, recur. Suppose, for example, that feldspar crystals, forming in a magma, should sink to a lower region where the magma is supersaturated. The conditions there are ripe for the formation of supersaturation twins. Special conditions obtain during the formation and early growth of a crystal nucleus which are particularly favorable to twin formation. When a crystal consists of merely two or three layers, the energy of an atom on its surface is not the same as that of the atom on the surface of an indefinitely large crystal. The energy summation consists of only a few terms rather than an infinite number and may be too small to closely approximate the converging value of the series. Conditions are thus different; they may be less unfavorable, if not positively favorable, to the formation of twins. As the crystal grows, the energy sum changes, or may even fluctuate during growth, until the crystal is large enough so that the energy sum has substantially converged. If growth now continues under equilibrium conditions, a twinned crystal has a higher energy and is subject to dissolution and reprecipitation on an untwinned crystal. If there is supersaturation, however, the chances are increased that the twinned crystals will grow to sufficiently large size that they will not readily redissolve. TRANSFORMATION TWINS It can be theoretically demonstrated that a pair of crystals connected by a high-low transformation possess related symmetries. The low temperature form has a symmetry which is a subgroup of the symmetry of the high temperature form. Now, in the transformation from the high form to the low form, the general structure remains the same, but some of its symmetry operations are suppressed. The low form merely forms at the expense of the high form by loss of symmetry. This can, in general, take place in such a way that the low form has more than one orientation with respect to the high form. This is indicated by the following analysis: the low form contains fewer coincidence operations than the high form. It can be transformed into itself in n ways, where n is the number of operations in its symmetry group. Since the group of the high form contains the group of the low form as a subgroup, the high form can be transformed into itself in mn ways. This means that the low form can be oriented in n indistinguishable ways in the structure while the high form can be oriented in mn indistinguishable ways in the structure. For any given orientation of the low form, there are m possible orientations of the high form. That is, there are m mutually different orientations of high and low form. High-low transformations take place as soon as the temperature of a region has reached the transformation level, and is propagated as a wave as rapidly as heat can be transmitted. Unless the crystal is extremely small, transformation nuclei may appear in various parts of the crystal spontaneously, particularly at the edges, and the transformation spreads from these centers. With falling temperature, the chance that any center shall assume the same orientation as a neighbor is 1/m. In general, then, a transformation from the high to the low form consists of a spontaneous formation of nuclei in m different orientations and these nuclei grow until they make contact with one another. From the mechanism of formation of these crystals, their contacts are often, though not necessarily, irregular. All individuals of the aggregate are either in parallel or different orientation. Those in different orientation are in twinned orientation with respect to one another. This follows from the fact that they could be brought into coincidence by one of the m operations of the high form which vanished in the formation of the low form. GLIDING TWINS It is well known that some crystals can yield to stress plastically by a process known as gliding. Two types of gliding are known, translation-gliding and twin-gliding.14 An untwinned crystal enjoys a state of lowest energy. If it should yield to stress by twin-gliding, then a higher energy is assumed. The energy is supplied, of course, by part of the work of deforming the crystal. In comparison, it should be noted that crystals which become twinned in the process of growth never attain a lowest energy state, while gliding twins are originally in a lowest energy state, but absorb energy in twinning and accordingly acquire a higher energy state. The higher energy of twins is substantially localized in the close vicinity of the twin boundary. The energy is essentially a surface energy or interfacial energy since it is associated with a discontinuity or interface between two homogeneous regions. Because of the special mechanism of the gliding process, the junctions between gliding twins are characteristically plane, although they may curve slightly and delimit the twin as a thin lens, especially if bending of the crystal is involved. If a crystal can form twins according to a certain law by growth twinning, it may or may not be able to form gliding twins according to this same law. While this will be discussed from a structural viewpoint later on, the energetics of the situation will alone be noted here. In glide twinning, each atom in the layer to start the twin is in a deep energy depression and must be caused to migrate to another depression. Energy barriers separate these depressions, otherwise they would not be depressions. If the energy barriers are comparatively low, glide twinning can be caused to occur. For example, if, for each atom, there exists a low energy path from normal position to twin position (say, a trough between depressions), then little energy is required to cause twinning shear between sheets. (For translation-gliding to take place, the energy trough must connect translation-equivalent depressions, not twin-equivalent depressions.) If, on the other hand, the depressions are surrounded by the highest energy barriers, then, to cause gliding is identical with causing the sheared sheets to separate, and thus the work of rupture (which may be cleavage) must be accomplished to cause gliding. Crystals with energy depressions so surrounded cannot be caused to glide, but rather break if sufficiently stressed. It goes without saying that the distribution of energy barriers is a function of structure. This general situation is a great restriction to twinning by gliding. Growth twinning is unrestricted by such potential barriers since each atom or cluster merely adds itself to the structure from a position in space which has a higher energy than either the normal location or the twin location. Thus many twin laws which are ordinarily possible for growth twins are impossible for gliding twins. When a crystal yields by twin-gliding, it does so in a peculiar sequence, and the process ordinarily leaves a characteristic record of its occurrence. If a stress having a shearing component in the glide plane is applied to the crystal in sufficient magnitude to cause overriding of the barriers, all parallel planes in the crystal are subject to the stress, yet gliding does not occur on all planes at once. What happens is that some fortuitous circumstance, possibly a flaw, defect, or even heat motion, reduces resistance locally. The crystal yields in this region and a twin lamella of minimum size forms delimited by two twin boundaries. In the neighborhood of these boundaries the energy is high, and consequently these regions are relatively yielding. Thus, with continued stress, gliding takes place in the next sheet to each twin boundary, and the twin lamella grows in width. Ordinarily, the lamella does not grow indefinitely, but is either blocked by a flaw, or fortuitous circumstances raise the resistance to shear in the original twin boundaries until resistance in some untwinned region is lower. When this occurs, further yielding by the crystal occurs by yield in a new place and there results the development of a new lamella. A crystal which has yielded plastically by twin-gliding is accordingly characterized by containing numerous parallel twin lamellae or bands. This repeated twinning is necessarily alternating twinning, and thus is polysynthetic twinning. The distribution of lamellae can be anything from regular to irregular, depending on the distribution and character of the "fortuitous circumstances" mentioned above. The widths of the bands depend on the extent of the deformation and distribution of "fortuitous circumstances." MISCELLANEOUS FEATURES OF TWINNING Parting and Replacement. - It has already been pointed out that a twin boundary is the locus of high energy. The work required to disrupt the crystal is partly represented by this increase in energy of the crystal at the boundary. If the boundary is plane, it is the weakest individual plane of all parallel planes, and if tension is applied to the crystal, the crystal breaks at the twin boundary (excluding cleavage). This constitutes parting. Thus twin boundaries are parting planes. (Other causes of "parting" are also recognized. 15) The high energy aspect of the twinning plane also localizes chemical action, so that chemical alteration and replacement tend to occur preferentially at twin boundaries. Such alteration, of course further weakens the resistance of the twin boundary to stresses and enhances the ease of parting.Relation of Twinning to Polymorphism. - Anyone who has been concerned with the mechanism of twin-gliding 6 has noticed that the structure in the twin boundary may be a polymorphic modification of the original structure. Aminoff and Broome7 have discussed the case of twinned sphalerite, which has the wurtzite arrangement in the twin boundary. Other examples could easily be cited. Indeed it is true in general that the structure in a twin boundary is at least a possible polymorphous alternative structure. This is because the atoms of most (though not all) polymorphous pairs have identical first ocordination spheres (some polymorphous pairs have different first coordination spheres) but different higher coordination spheres. This is exactly the situation in the twin boundary. In this sense, twin boundaries are cases of two-dimensional polymorphism. Thus the high energy of a twin boundary is related structurally to the high energy of an unstable polymorphous form.This suggests the following hypothesis: the possible growth twin laws of a crystal truly unstable under the conditions of its formation can include only such laws as have boundary structures of less stable polymorphic forms, and cannot include twin laws which have boundary structures of the stable modification. (Otherwise, the structure of the stable modification once started, would perpetuate the stable modification and the twin would cease to exist since the intergrowth would be one between stable and unstable modifications.) Should such a twin law be observed in an unstable crystal, the crystal is not a growth twin, or else the modification was not actually unstable under the conditions of formations. The possibilities of twinning in unstable crystals are thus restricted, and, in general, an unstable modification should display fewer twin laws than a stable modification. Relation of Twin Formation to Polymorphic Transformation. - Not only is twinning related to polymorphism, but a change from untwinned to twinned condition (as in glide twinning) is related to polymorphic transformation. From a structural point of view, two important kinds of polymorphic transformation can be recognized: (1) Transformations involving only a slight displacement of parts of the structure, of the order of heat motion. This kind of transformation may be termed a displacive transformation. It is of the high-low type and is called forth instantly by transgression of the critical temperature (example: low-quartz. to high-quartz). (2) Transformations requiring a bit-by-bit tearing down of one structure and a rebuilding of the bits to form a differently linked structure. This may be called a reconstructive transformation. It is of the sluggish variety because it requires a distillation of one structure into the other (example: quartz to cristobalite). Such transformations cannot be effected by simple displacement. There are also displacive and reconstructive varieties of twinning. In the displacive variety, the crystal and its twin boundary patterns may be made to transform into one another by simple displacement. Accordingly such twins can be formed by a high-low transformation or by twin-gliding. The possibility of a displacement is the structural equivalent of a low energy trough connecting energy depressions mentioned above. Other twinning is of the reconstructive variety, that is, the crystal can be transformed into its twin boundary only by a complete disintegration into bits and then reconstruction of its structure. Obviously, such twinning cannot result from high-low transformation or from the simple shear displacement of twin-gliding. Such twins can only be formed by the original precipitation of the twinned structure, and consequently reconstructive twins are limited to growth twins. This corresponds closely to the requirements for a reconstructive transformation. It might be pointed out that the albite twinning of plagioclase is of the displacive type, since the triclinic character of this crystal is due to a collapse of the monoclinic orthoclase structure such that oxygens coordinate with the small sodium atom. No relinking of the structure is required in passing from untwinned to twinned structure. It is thus possible that albite twins can arise by either transformation twinning or glide twinning, as well as by growth twinning. Guided by this reasoning, the writer and his students have experimentally produced polysynthetic twinning in albite by glide twinning. Relation of Transformation Twins to Unmixing. - In another place the writer has explained the formation, of segregate phase crystals in unmixing. 16 These are called forth in response to a requirement for ordering in the structure as the temperature falls. Transformation twins are also called forth by falling temperature, and often, if not always, this is equivalent to a requirement for some kind of ordering. Transformation twining is merely a degenerate case of segregate phase formation in which both original disordered and final ordered phases have identical chemical compositions.REMARKS ABOUT COMMON STATEMENTS OF THE CAUSE OF TWINNING One commonly finds statements equivalent to the following: "Twinning may be regarded as an unsuccessful attempt to establish a symmetry higher than that to which the simple crystal belongs." This kind of statement misses the meaning of symmetry and misses the significance of twinning. Symmetry, in essence, is a relation equivalent to the repetition of some geometrical feature. Any two similar things form a symmetrical pair, in a broad sense, since one is the repetition of the other. Crystallographic symmetry is merely a restriction of this notion to cases consistent with lattice translations. There is no virtue in symmetry such that atoms, coming together to form a crystal, should strive to attain it. There is no potential favoring it. Indeed, in the case of twins, the potential favors its absence. The writer is indebted to Dr. George Tunnell and Dr. J. D. H. Donnay for kindly reading this paper in manuscript and for offering constructive criticism of certain points raised in it. This should not be construed as necessarily committing them to the writer's views. NOTES 1 Donnay, J. D. H., Width of albite-twinning lamellae: Am. Mineral., 25, 578-586 (1940). 2 Emmons, R. C., and Gates, R. M., Plagioclase twinning: Bull. Geol. Soc. Am., 54, 287-304 (1943. 3 Donnay, J. D. H., Plagioclase twinning: Bull. Geol. Soc. Am., 54, 1645-1652 (1943). 4 Buerger, M. J., The temperature-structure-composition behavior of certain crystals: Proc. Nat. Acad. Sci., 20, 452 (1934). 5 Royer, M. L., Recherches expérimentales sur l'épitaxie ou orientation mutuelle de cristaux d'espèces différentis : Bull. Soc. Franc. Mineral., 51, 7-159 (1928). 6 Gruner, John W., Structural reasons for oriented intergrowths in some minerals: Am. Mineral., 14, 227-237 (1929). 6 Buerger, M. J., The plastic deformation of ore minerals: Am. Mineral., 13, especially pp. 40-41 (1928). 7 Aminoff, G., and Broomé, B., Strukturtheoretische Studien über Zwillinge, I: Zeits. Krist., (A) 80, 355-376 (1931). Taylor, W. H., Darbyshire, J. A., and Strunz, H., An x-ray investigation of the feldspars: Zeits. Krist (A) 87, 490-494 (1934) 9 Bragg, W. L., Atomic Structure of Minerals: Cornell University Press, Ithaca, N. Y., 52, 87, 119-121, 243-250 (1937). 10 Zachariasen, W. H., The crystal structure of sodium formate, NaHCO2: Jour. Am. Chem. Soc., 62, 1013 (1940). 11 Friedel, Georges, Leçons de cristallographie: Berger-Levrault, Paris, 421-483 (1926). 12 See Friedel, op. cit., p. 427. 13 See Friedel, op. cit., p. 434. * There should be no hesitance in discarding or amending older crystal theories, since the crystallography before about 1915 was concerned largely with lattice geometry, especially as inferred from outer form. Present day crystallographers have the advantage of a knowledge of the details of the structures of crystals, which gives them clearer insight into all crystal phenomena. To neglect this advantage is to continue yesterday's science. 14 Buerger, M. J., Translation-gliding in crystals: Am. Mineral., 15, especially pages 46-47 (1930). 15 Greig, J. W., Merwin, H. E., and Posnjak, E., Separation planes in magnetite: Am. Mineral., 21, 504-510 (1936). 16 Buerger, M. J., The temperature-structure-composition behavior of certain crystals: Proc. Nat. Acad. Sci., 20, 444-453 (1934).
|