| Home | AmMin | GMR | RiMG | Collectors Corner | Directory | Short Courses | |
|
|
|||||||

|
|
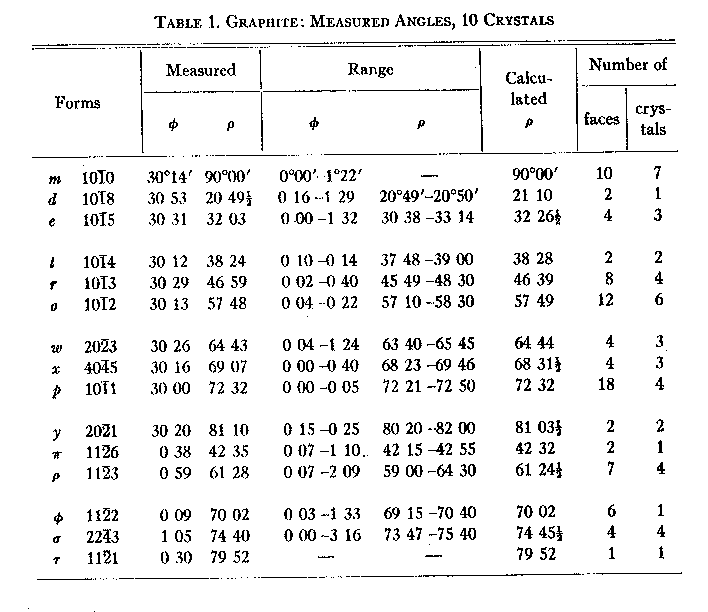
Volume 26, pages 709-717, 1941 CONTRIBUTIONS TO THE MINERALOGY OF STERLING HILL, NEW JERSEY: MORPHOLOGY OF GRAPHITE, ARSENOPYRITE, PYRITE, AND ARSENIC CHARLES PALACHE, Harvard University, Cambridge, Massachusetts.* GRAPHITE No satisfactory data for the morphological determination of the symmetry and elements of graphite have hitherto been published. Goldschmidt (1918), unable to decide between Kenngott's hexagonal interpretation of his meager data and the monoclinic interpretation of Nordenskjöld, gives both in the Atlas. The former has, however, been accepted by most authors and the mineral has been described as hexagonal-rhombohedral, the triangular striations commonly to be seen on the base determining its rhombohedral classification. Recent studies of the structure cell by x-ray methods lead to the conclusion that graphite is hexagonal (Bragg, 1937) and not rhombohedral, although a trigonal symmetry class is not excluded. The measurements presented in the following pages, made on graphite crystals from Sterling Hill, New Jersey, seem to the writer to yield a definite and unambiguous solution of this problem. Graphite is hexagonal with full symmetry. The graphite crystals from Sterling Hill occur in crystalline limestone in an association to be described on a later page. I am indebted for them to Mr. L. H. Bauer of Franklin, New Jersey, who found the material and isolated the best crystals. They are scales up to 1 or 2 mm. in diameter, the best ones, however, not exceeding 0.5 mm. The base is extremely brilliant, hexagonal in outline, with edges showing many facets, often very plane and bright, although striated edges are the rule. Of the hundreds of crystals studied, ten were completely measured and yielded the forms and angles shown in Table 1. Four of these crystals were very simple in form and gave closely agreeing measurements for three forms only besides the basal pinacoid, which are regarded as definitely proving the hexagonal symmetry of graphite. They are summarized in Table 2. But one of these crystals showed measurable faces at the lower end, and it was unfortunately lost in attempting to reverse it on the goniometer. Figures 1, 2 and 3 represent respectively crystals 1, 3 and 4 of Table 2 in approximately their actual development. TABLE 1. GRAPHITE: MEASURED ANGLES, 10 CRYSTALS
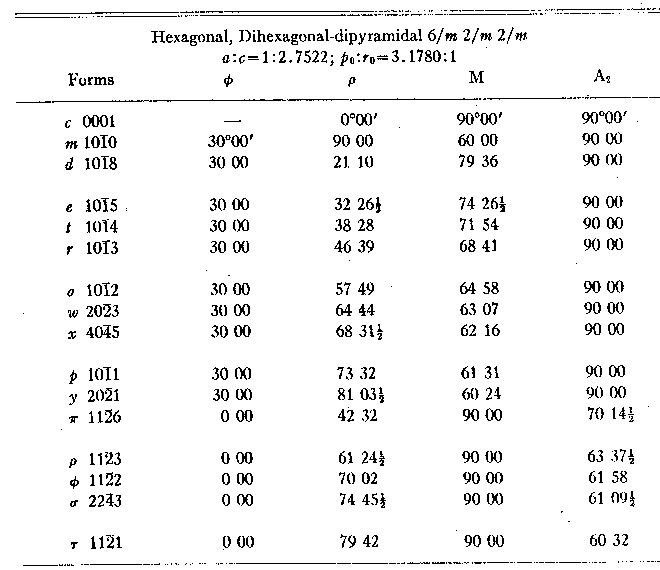
The other measured crystals were more complex. Figure 4 illustrates one of them and it is evident that individual forms are irregularly developed, no one pyramid having all its six faces present. But the distribution in this and in every crystal is not systematically trigonal but random. It is also true that other reflections were obtained from some crystals which were not in the dominant zones and which could not be simply indexed in the projection. But these were always subordinate to the prevailing hexagonal distribution. From the mean values for the position angles shown in Table 1 the elements were calculated, using 69 faces of 11 forms on 10 crystals. The resulting value, po=3.1780, c=2.7522, is taken for the calculation of the angle table, Table 3.
TABLE 2. MEASUREMENTS OF 4 CRYSTALS OF GRAPHITE TABLE 3. GRAPHITE:
ANGLE TABLE
The elements calculated from x-ray measurements are po=3.170, The commonly accepted elements of graphite based on Kenngott's (1854) original measurements are, if c be doubled, po=3.2006, c=2.7718, but regarding this value see the remarks on a later page. Confirmation of the results obtained from these measurements was found on a single crystal of graphite from Ticonderoga, New York, shown in Fig. 5. Although of much poorer quality than the Sterling Hill crystals, it gave mean angles for two forms which are comparable:
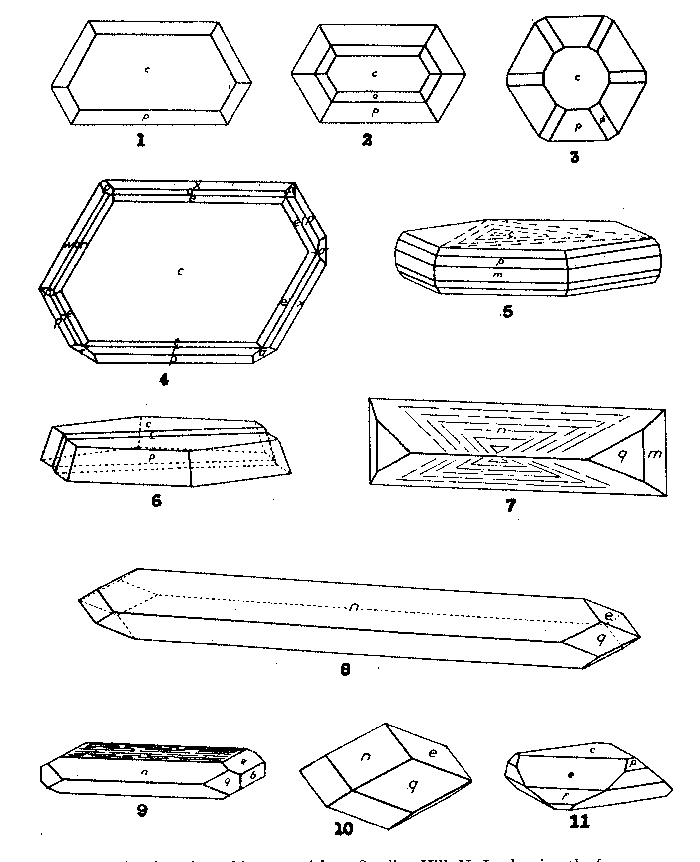
FIG. 1. Plan of graphite crystal from Sterling Hill, N. J., showing the forms
c{0001} and p {10 FIG. 2. Plan of graphite crystal from Sterling Hill, N. J., showing the forms
c{0001}, p{10 FIG. 3. Plan of graphite crystal from Sterling Hill, N. J., showing the forms
c{0001}, p{10 FIG. 4. Plan of graphite crystal from Sterling Hill, N. J., showing irregular disposition of faces of the forms.
FIG. 5. Graphite crystal from Ticonderoga, N. Y., showing full hexagonal
symmetry with the forms c{0001}, m{10 FIG. 6. Graphite crystal from Sterling Hill, N. J., showing the forms c
{0001} and p {10 FIG. 7. Crystal of arsenopyrite from Sterling Hill, N. J., showing the forms m{110}, q{210} and n{101}. FIG. 8. Crystal of arsenopyrite from Sterling Hill, N. J., elongated on b showing q{210}, e{012} and n{101}. FIG. 9. Crystal of arsenopyrite from Sterling Hill, N. J., showing b{010}, q{210}, e {012}, n {101} and a pseudobase due to striation. FIG. 10. Crystal of arsenopyrite from Sterling Hill, N. J., equant, with q{210}, e{012}, and n{101}. FIG. 11. Crystal of native arsenic from Sterling Hill, N. J., showing c{0001},
e{10
This crystal was the only one on which the faces of the lower end could also be measured; they were so placed as to indicate a horizontal plane of symmetry. Forms. The base {0001} is the dominant form on graphite from all
localities. Generally it has splendent luster and is invariably used for
orientation of a crystal on the
goniometer. {10 Twinning. In selecting crystals for measurement, those whose base was
quite free from striae were sought for. The vast majority of the crystals
showed striations on the base in one, two or three directions, always in
diagonal relation to the hexagonal outline. Two were measured upon
which a single twin lamella traversed the crystal with a sharp plane face
of the pinacoid in twin position, making an angle to the base of about 20°, as shown in Fig. 6. This corresponds to a face as
twin plane of the
form {11 Kenngott stated that all his measurements were approximate, particularly that of the form parallel to the basal striae which he took as unit rhombohedron and on which he based his element. The fact that the c-axis so derived is so nearly in accord with that of our position as shown on a preceding page is due wholly to chance. The following tabulation shows the angles of his three forms compared with the nearest calculated angles of the two series of dipyramids in our position.
The agreement of Kenngott's angles with those of our first column is perfect, but the relation of his forms to the striae on the base makes it impossible to accept this agreement. His values must be compared to our second column and there the agreement is very poor. We can only blame the quality of his crystals. Kenngott did not figure his crystals of graphite, but in Descloizeaux we find a figure drawn, as stated, from Kenngott's data. There is nothing to be found in Kenngott's paper to show that the habit of this figured crystal is true to nature. But it so happens that the crystal is drawn in the position adopted in this paper, and the relative proportions of the forms, especially of the second order pyramid, shown with three faces only since it was regarded as a rhombohedron, is strikingly like our Fig. 4. Thus, also by chance, the only figure of a graphite crystal extant is now justified by new observations. During the progress of this study, Dr. M. A. Peacock examined the projections of some of the Sterling Hill crystals of graphite and afterwards drew up a projection, based on the elements determined by x-ray study. In this projection he introduced the lattice planes with greatest spacings which were to be regarded as probable crystal forms. The forms so indicated are the forms of Table 1 bearing the letters c, m, e, t, r, o, p, y, p, φ, and τ. The only form in his projection not found by any observer is the second order prism. Our list has, in addition, five forms d, w, x, , π, and σ which are all weak and infrequently occurring. The comparison of the completed form list with Dr. Peacock's projection, quite forgotten in the year or more during which the study has extended, revealed a parallelism so close as to seem worthy of record as an additional evidence of the correctness of the present interpretation of graphite morphology. Paragenesis of the Sterling Hill Graphite In May 1937 there were found on the 900-foot level of the mine at Sterling Hill, New Jersey, specimens showing an entirely new paragenesis for this locality. Samples were presented at that time to the Harvard Mineralogical Laboratory by Mr. L. H. Bauer, and repeatedly in the succeeding years the same donor has sent selections of carefully isolated crystals of the several minerals. Description of the material has been so long delayed because only recently were really decisive crystals of graphite found which finally solved the puzzle of its morphology. The specimens consist of massive, coarsely crystalline limestone, with irregular impregnations of the following minerals: graphite, native arsenic, realgar, pyrite, arsenopyrite, diopside, and a few needles of either stibnite or a lead sulphantimonide. Since all of these minerals are set free without sensible injury by solution of the limestone in dilute hydrochloric acid, an abundance of the crystals of most of them can be obtained with ease. Arsenic, realgar and the antimony compound are quite new to the Franklin region.The chief interest centered in the brilliant scales of graphite which were found in considerable numbers in the solution residue. The scales range in size from minute specks to plates 2 mm. in diameter and 0.5 mm. in thickness. The base is extremely brilliant and the edges of the hexagonal plate show many facets. The details of their crystal form have already been presented. Most of the graphite crystals are distorted, having suffered from movements in the embedding calcite which has caused the development of numerous gliding-plane: twin lamellae in both calcite and graphite. Occasionally, however, the graphite has escaped all distortion or at least shows only a single twin lamella. The graphite crystals are generally quite free but may be partly embedded in arsenopyrite, in arsenic or in diopside.ARSENOPYRITE Next in abundance and beauty of the isolated crystals is arsenopyrite. The crystals, while minute, are of amazing brilliance and perfection of form. They present few crystal forms but range in habit from needles of hair-like fineness to stout prisms or flattened plates. In dimensions they commonly range from 0.5 by 1 mm. to 1 by 2 mm. They are chiefly bounded by the forms** m{110}, g{210}, e{012}, and n{101}. Of these n is generally largely developed and the hair-like crystals are elongated parallel to it. Commonest type has n and q alone, or with m as in Figs. 7 and 8, the latter an attempt to delineate the hair-like needles. By flattening parallel to one pair of planes of n the crystals take a platy form. Another mode of flattening is by development of a striation zone over the basal edge as in Fig. 9, producing a dull pseudobase; e is also common and may be equally developed with n and q as in Fig. 10. Sometimes but one face of e is present. There is a strong tendency for striae to form between e and n which is generally accompanied by a similar striation between n and q as shown in Fig. 7. This latter is often so deep as to eliminate the prism planes. Fig. 9 shows a rare type in which {010} truncates what is commonly an acute end.Other forms measured on single crystals or in single faces or pairs are {610}, {430}, {111}, {113}, {416}, and {212}. It is hoped that an analysis will be made of these exceptional crystals of arsenopyrite.
PYRITE Pyrite, much less abundant in the residues than arsenopyrite, is present in model-perfect crystals of varied habit. The following combinations were noted: {100} and {111} ; {120} alone and with {111}; a few very brilliant crystals showing {210}, {111}, {110} and {112}.ARSENIC Arsenic is present in but few grains and crystals. However, one was found to be measurable which yielded the forms c{0001}, e{00Realgar is in rude prismatic individuals with ragged terminations which admit of no measurement.Needles of an antimony compound have been mentioned. Too little was secured to enable its satisfactory determination. Diopside is the most abundant of the residue constituents. It forms irregular clusters of rounded crystals, white in color and identified only by its optical properties, since the crystals were too ill defined to be interpreted. In the writer's genetic classification of the Franklin minerals (Palache, 1929) a subgroup was set up called "pneumatolytic products" which was stated to be practically confined to the Franklin deposit. This new paragenesis appears to belong to this group and extends its range to Sterling Hill. REFERENCES BRAGG,
W. L., Atomic Structure of Minerals, 54 (1937).
NOTES * Contribution from the Department of Mineralogy and Petrography, Harvard University, No. 248. ** The forms, symbols, and drawings are in the new position required by the results of the study of this mineral by Buerger (1936).
|
||||||||||||||||||||||||||||||||||||||||||