| Home | AmMin | GMR | RiMG | Collectors Corner | Directory | Short Courses | |
|
|
|||||||

|
|
Volume 63, pages 17-27, 1978 Characters of quartz fibers1 CLIFFORD FRONDEL. Department of Geological Sciences, Harvard University Cambridge, Massachusetts 02138Abstract
X-ray and piezoelectric techniques confirm that the common direction of
elongation of' microscopic quartz fibers is along a polar <11
Both quartz fibers and single crystals elongated along [11 Right- and left-handed twisted quartz fibers appear to be equally abundant, although seeding effects may locally give rise to a large preponderance of one enantiomorph. Data on 27,043 quartz single crystals also indicate that the two enantiomorphs are equally abundant.
The dimensional elongation of quartz fibers and single crystals along one
direction of a three-fold symmetry-equivalent set, (11 It is suggested that the general occurrence of quartz as microscopic fibers in low-temperature environments, and as macroscopic euhedral or anhedral crystals in higher temperature environments, arises in factors determining the incidence, density, and orientation of dislocations in a quartz matrix rather than through the crystallization kinetics of the solution itself. Introduction Among the more common types of occurrence of fibrous quartz are sedimentary rocks (chert), concretionary masses (flint), replacement and alteration bodies in rocks, and varied crevice and cavity fillings such as crustiform aggregates, geodes, and agates. The latter occurrences generally pass under the name chalcedony. What is primarily of interest here are the characters of quartz fibers that have nucleated from solution at an interface, as upon a planar surface or the wall of a spheroidal cavity, to form parallelfibrous or radially-fibrous aggregates. Aside from facilitating the study of the fibers in an experimental sense, this condition is essential to the recognition of fiber characters such as polar orientation to the site of nucleation and stereospecific twisting. Non-centric properties of quartz
With regard to pertinent aspects of the crystallography of quartz, the
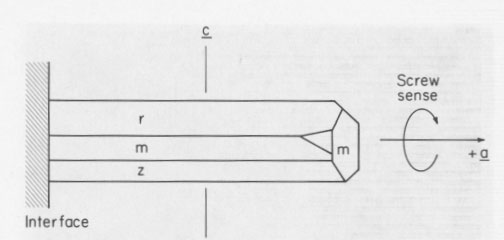
structural polarity of the twofold symmetry axes, or <11 Structurally, the Si and O ions are arranged in special positions in the enantiomorphous space groups C312 and C322. The enantiomorphism arises in helical arrangements of the Si and O ions along the [0001] direction. This arrangement and the associated optical activity are lost when the structure is dissolved or melted. The chirality of quartz as described by conventional morphological and optical rotatory criteria is opposite to that of the crystal structure. Fiber elongation
The common direction of fiber elongation as determined by X-ray diffraction and
piezoelectric techniques is along one of the polar <11
In the formation of fibrous quartz, the direction of elongation as predicted by
periodic bond-chain theory (Hartman and Perdok, 1955; Hartman, 1973) is related
to chains of strong Si-O-Si bonds running through the crystal structure. The
strongest of these chains are in the (1120) and [0001] directions. A problem
arises here in that the <11 Polar orientation
Since the [11 The microscopic fibers that constitute chert and flint are randomly arranged as seen in thin section. Plates cut from such aggregates did not give a piezoelectric response. Optically the fibers generally are length-fast; they hence are elongated in the (0001) plane, but the identity of the specific direction therein is not known.
The polar orientation is viewed as a rate-of-growth effect connected with the
dislocations to which the fiber elongation itself is ascribed. It is believed to
derive from the different core structure of screw dislocations propagated in
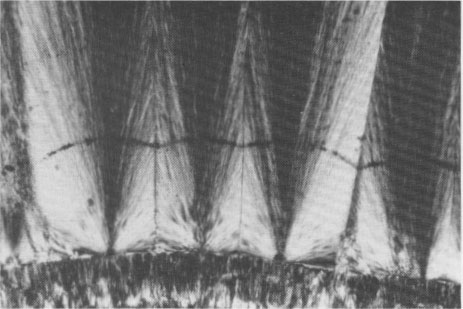
opposite senses along [11 When the faces terminating the fibers can be discerned they are found to belong to either {1010} or to a {1011} or {0111} rhombohedron. It may be noted that fibers terminated by these or other non-polar forms, if free from dislocations, would have identical growth rates regardless of the polar sense of the axis. Solubility control has been suggested by Becke (1889) and Holzner (1927) for examples of polar orientation in hemimorphite and other crystals. During the random nucleation of a polar substance upon an interface, those nuclei that by chance have their greater rate-of-solution polar vector suppressed by attachment at the interface would have, in effect, a lower bulk solubility. They hence should nucleate first and yield a preferred orientation. This mechanism seems unlikely in quartz, since the greater polar rate of solution vector comprises a three-fold set. Solubility control also has been suggested by Johnson (1907) for crystals twinned by reflection across the plane perpendicular to a polar axis. Here, as a general rule, the polar vectors of greater rate of solution in the twinned parts point toward the surface of juncture. Dauphine twinning in quartz appears to follow this relation. Whatever the mechanism involved, the polar orientation of quartz fibers is a physical effect that is independent of the chemical or structural nature of the interface itself. In this it differs from the polar orientation of elongate organic molecules and long-chain biopolymers containing hydrophilic and hydrophobic substituent groups at opposite poles. A review of this subject is given by Tanford (1973). Although the opposite ends of polar quartz fibers are chemically identical, their adsorptive behavior, such as with regard to (OH)- and H;, may be different. Stereospecific twisting Twisting around (11 The orderly twisting of quartz fibers was first noticed and explained optically by Michel-Lévy and Munier-Chalmas (1892), and there are numerous incidental observations in later literature. The main study of twisting in fibers generally, however, has been in connection with the so-called banded spherulites of organic high-polymers (Bernauer, 1929; Geil, 1963; Price, 1959; Keller, 1955), and in whisker crystals of metals and other substances. In parallel-fibrous and radially-fibrous quartz aggregates, as examined in thin section cut parallel to the fiber elongation, the twisting appears in polarized light as a succession of zero birefringence optical extinction bands extending along the fiber length (Fig. 1). The bands represent the identity period of the twist that brings the optic axis (at right angles to the fiber elongation) parallel to the microscope axis. General treatments have been given by Keller (1959) and by Keith and Padden (1959) of the optical effects produced in fibers by the rotation of uniaxial and biaxial indicatrices in both twisted and helical arrangements. Quartz normally is uniaxial, but sometimes shows an anomalous biaxial character. In such instances, as earlier noted by Jones (1952) and others, the obtuse bisectrix X is along the fiber length, with 2 V variable 10° to 30°.
The twist period in quartz fibers, based on the measurement of several hundred examples, ranges from about 20 to 700 microns. Longer twist periods, in the mm to cm range, apparently occur, but could not be measured optically either because the fiber was too short or extended outside the area of the thin section. Over 100 successive twists have been observed along a single fiber. The twist period ordinarily is uniform along the fiber length. A variation is occasionally noted close to the point where crystallization initiated. Here the twist period may rapidly increase to larger values. An abrupt variation also has been noted at the terminal end (Fig. 2). In some instances twisting along the fiber length may be interrupted by one or more untwisted zones. The twist sense of the fibers is found to be either to the right or left. It can be determined by the technique of Bernauer (1926), involving rotating the fiber in polarized light on a universal stage in a prescribed manner. The thickness of the fibers as determined by electron microscopy is in the range from about 0.05 to 1 micron in most parallel-fibrous and radially-fibrous aggregates. The range is somewhat smaller in chert and flint. The thickness extends up to 10 microns or more in some hydrothermal vein fillings and crustiform types formed at relatively high temperatures. The twist period tends to increase with increasing fiber thickness although, as noted beyond, the primary control appears to be the temperature of crystallization.
The fiber length ranges up to several cm in some geodes and agates. The individual fibers usually are grouped into bundles from a few microns to over 50 microns in thickness. Occasionally the bundles appear to be helically twisted on a coarse scale. This feature also has been noted by Reis (1916).
The zig-zag appearance of the twist extinction bands is mainly caused by a
slight angular divergence or a slight lengthwise displacement between adjacent
fiber bundles. If these differences are large, the twist extinction has a mosaic
or blotchy appearance or it may be obliterated. Identical features are shown by
the banded spherulites of organic high-polymers. The twist extinction bands are
relatively poorly developed in crustiform types from hydrothermal veins, and
generally are not observed in the individual fibers of random or feathery
aggregates. It is difficult to decide in many instances whether twisting is
absent or if it has been obscured. In any case, twisting is a very common
character of quartz fibers elongated along [11 Twisting around
[11
Large twisted quartz crystals were first noticed by Weiss (1836) and there are
numerous later descriptions, notably by Tschermak (1894), Rosicky (1933),
Friedlaender (1951), and Lemmlein (1936, 1937). In large quartz single crystals,
the sense of the twist around [11 Direct measurement of the pitch of 228 crystals examined in various museum collections are in the range from 8.5° to 0.50° per cm. These values correspond to calculated twist periods of 21 to 360 cm. Values in this range also have been reported in the literature. Some crystals apparently have twist periods extending to 500 cm or more, but the measurement of very small pitches by optical goniometry becomes uncertain because of surface irregularities.
Twisted single crystals occur as euhedral individuals, more or less elongated
along [11
The terminal prism edge at the free end often has a slight S-shaped inflection to the right or left in the same sense as the twist. Trigonal trapezohedral faces usually are present and are of relatively large size. The perfection of the crystals varies considerably. The surfaces of some are smooth and continuous (Tschermak's closed type), other crystals are composite, and composed of partly merged individuals (open type). In thin section the most perfect crystals show undulose extinction, and afford X-ray single crystal photographs with uniformly stretched-out reflections. As with the fibers, there is a rough tendency for the twist period to increase with increasing crystal size. Most of the known occurrences are in hydrothermal quartz veins, cavity deposits of the Alpine type, and pegmatites. Twisting around [0001] Quartz fibers elongated along [0001] are rare. They can be identified optically (length-slow), but the presence of twisting around [0001] cannot be recognized optically in the uniaxial case. A few instances of twisting around [0001] in large single crystals have been noted by Tschermak (1894), Lemmlein (1936, 1937), Frondel (1936, 1962), and Sadanaga and Bunno (1974). Ten additional instances were found in the course of the present study. The twist sense has been reported as in the same sense or the opposite sense as the morphological hand. Nearly all instances are of the latter type. Identification of the twist sense sometimes is ambiguous because of the presence of twinning. The twist period, in terms of a 120° turn, is variable. In the specimens examined here it ranged from about 54 to 800 cm. The maximum turn observed was about 45° over a length of 21 cm. The occurrences are all from high temperature environments. The crystals usually are relatively elongate along [0001]. Origin
The [11 The types of occurrence include geodal concretions and crusts produced in the meteoric circulation and by weathering processes, cavity fillings formed during the chloritic and zeolitic stages of post-magmatic hydrothermal action in basic igneous flow rocks, gas cavity fillings formed in rhyolitic flows and welded tuffs and in basaltic flows, gash veins in sandstone and quartzites, cavity and vein fillings of the so-called Alpine type, quartz veins containing silicates and sulfidic minerals of moderate to high temperature affiliations, pegmatites, and miarolitic cavities in granitic rocks. In a general way, the twist period and the crystal size increase and the incidence of twisting decreases in the order given. The range of temperature represented for the crystallization of the quartz in these occurrences is conjectural. Study of liquid inclusions in the twisted crystals would be informative of the actual temperature of crystallization.
It is not known if the twist period is a linear or more complex function of temperature, or if the relation is directly with the temperature or with some character of the crystallizing solution that is temperature dependent.
There is also a marked variation in the incidence of twisting around [11
The twisting of quartz is believed to derive from screw dislocations with their
Burgers vector along the direction of elongation and twisting. The primary slip
systems in quartz have Burgers vectors along (11
A structural model for the propagation of screw dislocations along [11 Whisker crystals of centrosymmetric substances show twisting to the right or the left depending on the chance sense of the initial dislocation. The sense of the twist or stress field produced is opposite to the screw sense of the controlling dislocation. In twisted whisker crystals the twist period has been observed to vary from small to immeasureably large values in the same substance. Features such as the temporary cessation of twisting along the whisker axis, such as seen in quartz fibers, also have been observed. The twisting of whisker crystals and of planar organic spherulite fibers apparently is primarily a function of temperature (Geil, 1963; Keller, 1959), although fiber or crystal thickness and the degree of supersaturation have been discussed in this connection. A relation between crystal size and twist period in quartz single crystals has been sought by Billows (1909), Rosicky (1933), and Lemmlein (1936, 1937), but the observed relation is very crude. It is often found, for example, that separate crystals of the same thickness or overall dimensions will vary in twist period by a factor of 2 or more. The degree of supersaturation seems a more likely control for both the crystal size and the twist period. It influences the rate of nucleation, or ultimate average crystal size, and as found by Kozlovskii (1962) the step height of screw dislocations increases with decreasing supersaturation. Fiber enantiomorphism
If the nucleation of quartz as right or left enantiomorphs is a matter of
chance, the two enantiomrophs should be equally frequent. This appears to be the
case. The chirality of 27,043 large quartz crystals has been determined by
morphological, optical rotatory, or etching techniques: 13,481 are left-handed
and 13,572 are right-handed. The data have been drawn from studies by Gross
(1972), Lemmlein (1944), Heritsch (1952), Bussiere and Maisonneuve (1971), C. S.
Hurlbut (private communication, 1549 left- and 1551 right-handed), and other
sources cited by Frondel (1962). Because of presumed seeding effects some local
quartz populations in igneous rocks are predominantly right or left (Heritsch,
1952; Bussiere and Maisonneuve, 1971). Of 301 single crystals twisted around [11 It is found that most aggregates of twisted fibers are more or less equal mixtures of the two enantiomorphs. In some instances, however, sizeable areas of fibrous geodes and agates, as seen in section, are all of the same hand, right or left. Occasionally these objects apparently are wholly of the same hand. A sectoral distribution of enantiomorphs has been observed in some planar organic spherulites (Keith and Padden, 1959).
Periodic fiber striations A poorly understood feature occasionally seen in quartz fibers is a uniformly spaced series of striations at right angles to the elongation of the fiber aggregates. The striations and the associated optical effects were first described by Jones (1952). The striations appear dark in both ordinary and polarized light (Figs. 5 and 6). A similar effect has been described by Keith and Padden (1958) in spherulites of organic high-polymers. The striations apparently represent internal boundaries of different optical density at which light is in part scattered and totally reflected and across which crystallographic continuity is maintained. What is seen is the optical effect and not the boundary itself. Examination by both transmission and scanning electron microscopy and, in the case of very broad striations, by optical microscopy does not clearly indicate the nature of the boundaries. Minute inclusions of foreign material are seen in some instances. The spacing of the striations usually is about 1 to 3 microns, but ranges down to the limit of optical resolution and upwards to 100 microns or more. It often is constant over long sequences. In one instance over 8,000 successive striations spaced approximately 2 microns apart were observed. When the fiber length is in the plane of a relatively thick section the regularly spaced striations act as optical phase gratings and produce strongly polarized diffraction colors in transmitted light (Raman and Jayaraman, 1953, 1955; Jayaraman, 1953). So-called iris agate is of this nature. The effect is diminished and the striations appear diffuse with increasing inclination of the fibers to the plane of the section. The striations also may appear bordered by a bright line, depending on their attitude and the manner of illumination. The optical density or apparent width of the striations is a function of the scattering power of the boundary. It usually is quite constant, but sometimes varies without changing the center-to-center spacing of the striations. A lengthy sequence may then involve orderly alternations of dark (D) and faint (F) striations such as . . . DFDF ... DFFFDFFFD..., or ...DDFFFFDDFFFFDD... (Fig. 7). Sequences also may be interrupted by gaps, the gaps either uniformly spaced or varying in size along the fiber length. In twisted fibers there is no apparent relation between the spacing of the striations and the twist period. The ratio of the two was found to vary between about 30 to 1 and 120 to 1 in about 30 measured examples from various localities. In some but not all instances, gaps in the striation sequence are accompanied by gaps in the twisting.
The feature has been observed only in closed systems, that is, where fibrous quartz has been deposited by solutions infiltrating closed cavities to form radially-fibrous geodes or agates. As with the twist extinction bands, the striations have a zig-zag appearance when traced across adjoining fibers or fiber bundles and have proportionally the same off-set. The uniformity of the spacing over long sequences would seem to preclude periodic variation in some gross character of the solution, such as temperature or pH, that is recorded on the fibers. Fiber participation must be involved to the extent of modulating some external factor. Possibly pyroelectric charges at the growing tips of the fibers, generated by thermal strain attending diffusion of the latent heat of crystallization away from the interface, have influenced the growth mechanism. Rapid growth under non-equilibrium conditions would then seem requisite. Torsional strain associated with screw-dislocations also might excite piezoelectric charges. Periodic interaction of growing fiber tips charged by adsorptive processes with oppositely-charged colloidal particles of foreign material in the solution, such as hydrous iron oxide, is another possibility. Etched sections of quartz single crystals occasionally show irregularly spaced sequences of thin growth bands that differ in their content of (OH) and in their indices of refraction (Bambauer, 1961; Bambauer et al., 1961; Kats, 1962; Bambauer et al., 1969). Infrared and thermal studies of chalcedony (Pelto, 1956; Brunner et al., 1959) show that the small amounts of water generally present include (OH), together with molecular water, although the site or sites in which it is located are uncertain. Zoning in terms of (OH) content along the fiber length thus also comes into question here.
Periodic phenomena also appear in single crystals of the amethyst variety of
quartz. Here alternating bands of right- and left-handed quartz twinned on the
Brazil law, of uniform thickness in the micron range of size, extend over long
sequences. Since the striated fibers are found to have a uniform piezoelectric
response, the suggestion that they are polysynthetic twins on the Japan law
(Raman and Jayaraman, 1955) or on the Dauphine or Brazil laws can not apply.
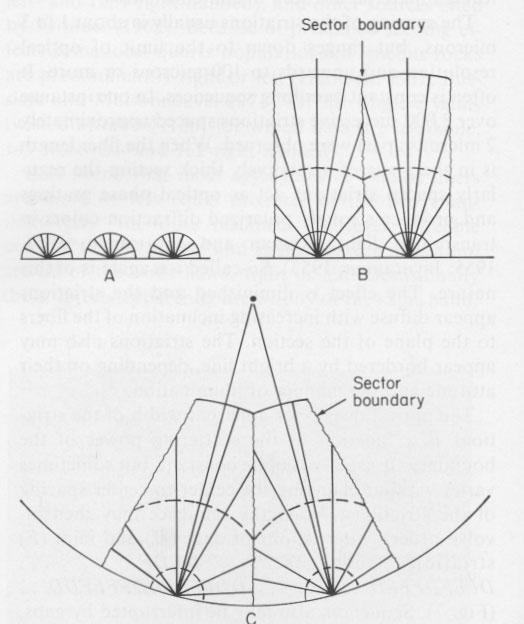
These laws reverse the polarity in the successive parts along [11 Fiber aggregates In the manifold varieties of fibrous quartz the two main modes of aggregation are either random or spherulitic. Random orientation of essentially isolated fibers is characteristic of chert and flint, although some degree of organization around the site of nucleation is shown by the occurrence of sheaflike, fan-like, sub-radial, and occasionally spherulitic forms. In fibrous quartz aggregates that have formed by crystallization from solution at an interface, the fiber organization generally is not random. The three cases commonly observed are, in idealized form: nucleation at a single point on the interface, usually giving rise to a hemispherical, divergently-fibrous spherulite; nucleation at many points on a planar interface, usually affording a parallel-fibrous crust; and nucleation at many points on the walls of a spheroidal cavity, usually forming an inwardly convergent radial aggregate. Examination under the microscope of thin sections cut across the interface of inwardly radial aggregates (chiefly geodes and agates) and parallel-fibrous crusts shows that crystallization generally begins not as isolated fibers, although this sometimes appears to be the case, but as minute, hemispherical, divergently fibrous spherulites scattered over the interface (Fig. 8). As the spherulites grow in size they abut and interfere laterally, with those fibers more nearly perpendicular to the interface surviving competition. At a planar interface the end result is a crust of fibers in approximately parallel array perpendicular to the interface (Fig. 9A, B). In the spheroidal case the fibers become radial (Fig. 9C). In neither case does the final arrangement resemble a spherulite, especially in agates with a central cavity, but the process of nucleation is spherulitic. In the spheroidal case, the surfaces of juncture of adjoining spherulites also converge inwardly, often in complex patterns, as seen in cross-section, depending on the actual shape of the cavity and the number and arrangement of the sites of nucleation (Figs. 10 and 11 ). This gives rise to the turtleback structure seen in cross-sections of some agates. When distinct twist extinction bands and periodic striations are present they are continuous throughout the various sectors (Fig. 12). Initially they are concentric around the various sites of spherulitic nucleation, but as growth continues they ultimately appear as shells concentric to the walls of the cavity. The degree to which these features are, so to speak, in phase in adjoining sectors or fiber bundles, giving a more or less zig-zag appearance, must depend on the timing in the formation of the initial spherulites. If the fibers in adjoining sectors are inclined at different angles to the plane of the thin section the continuity of the twist bands is broken, and at large angular differences they may seem to stop at the boundary. Sometimes finely disseminated foreign material becomes included during the growth of the fibers, giving thin pigmented bands that serve as marker horizons (Figs. 8 and 11). It should be added that agates have many additional features, not wholly relevant to the present matters, such as successive generations or bands of fibers not in crystallographic continuity with other bands.
Quartz crystals in geodes and agates
A quite general feature of fibrous-quartz cavity fillings, found in all types of
occurrence, is the presence of a central opening that is crusted by or filled
with macroscopic quartz crystals. The crystals range up to a cm or more in size
and are characterized by the small development or absence of prism faces and the
dominance of {10
This matter points up a more general question. Quartz tends to crystallize in low-temperature environments as microscopic fibers, to form chert, flint, and the varied forms of chalcedony, and in high-temperature environments to form macroscopic euhedral or anhedral single crystals. Two different characters are involved. One is the difference in size, to which attention usually is drawn, and the other is crystallographic. The latter comprise the dimensional elongation along one direction of a symmetry-equivalent set to form a fiber in the first place, the polar orientation, and the general occurrence of stereospecific twisting. These features indicate the pervasive role of dislocations in the fibers. The spherulitic manner of crystallization of the fibers, to the extent that this derives from imperfections in the initial crystal nucleus, also may be controlled by dislocations. The unlike modes of crystallization in the two temperature regimes may arise in factors determining the incidence, density, and orientation of dislocations in a quartz matrix, rather than wholly through the crystallization kinetics of the solution itself.
Acknowledgments Access to study material was kindly facilitated by Peter Embrey and A. A. Moss of the British Museum (Natural History), Paul Desautels of the Smithsonian Institution. Vincent Manson of the American Museum of Natural History, H. A. Stalder of the Natural History Museum, Berne, and Eric Welin of the Natural History Museum, Stockholm. Peter Keller of the Los Angeles County Museum and Erle Collins, San Francisco, supplied many agate specimens. Much of the material examined came from the Harvard University Mineralogical Museum. Appreciation also is expressed to Harold Thompson and Maurice Campot of the Department of Geological Sciences, Harvard University, for aid in the preparation of thin sections and in making piezoelectric measurements. Steven Richardson of the Smithsonian Astrophysical Observatory, Cambridge, contributed to the X-ray studies. The writer is indebted to John M. Christie, University of California, Los Angeles, for discussions of dislocation theory. References Ashbee, K. H. G. (1973) The Peierls force in crystalline quartz. Am. Mineral., 58, 947-948. Baeta, R. D. and K. H. G. Ashbee (1969) Slip systems in quartz. Am. Mineral., 54, 1551-1573, 1574-1582. Bambauer, H. U. (1961) Spurenelementgehalte and y-Farbzentren in Quarzen as Zerklüften der Schweizer Alpen. Schweiz. Mineral. Petrogr. Mitt., 41, 335-369. G. O. Brunner and F. Laves (1961) Beobachtungen über Lamellenbau an Bergkristallen. Z. Kristallogr., 116, 173-181. _______ and (1969) Light scattering of heat-treated quartz in relation to hydrogen-containing defects. Am. Mineral., 54,718-724. Becke, F. (1889) Die Kristallform des Traubenzuckers and optische aktiver Substanzen im allgemeinen. Tschermaks Mineral. Petrogr. Mitt., 10, 464-499. Bernauer, F. (1926) Über Zickzackbänderung and verwandte Polarizationserscheinungen an Kristallen and Kristallaggregaten. Neues Jahrb. Mineral., Beil. -Band, 55, 92-143. _______ (1929) Gedrillte Kristalle. Borntraeger, Leipzig. Billows, E. (1909) Associazioni regolari di cristalli della stessa specie. Associazoni elicoidale del quarzo. Rioista Mineral., 37, 3-112. Blacic, J. D. (1975) Plastic mechanisms in quartz: the effect of water. Tectonophysics, 27, 271-292. Braitsch, O. (1957) Über die natürlichen Faser- und Aggregationstypen beim SiO 2, ihre Verwachsungsformen, Richtungsstatistik und Doppelbrechung. Beitr. Mineral. Petrogr., 5, 331-372.Brown. C. S., R. C. Kell, L. A. Thomas, N. Wooster and W. A. Wooster (1952) The growth and properties of large crystals of synthetic quartz. Mineral. Mag., 29, 858-874. Brunner, G. O., H. Wondratschek and F. Laves (1959) Uber die Ultrarotabsorption des Quarzes. Naturwissenschafien, 24, 661. Bussiere, P. and J. Maisonneuve (1971) Repartition des varietes enantiomorphes du quartz clans les granites de la Tefedest, Algerie. Trau. Lab. Geol. Mineral., Univ. Clermont Ferrand, 18, 1-24. Christie, J. M. and H. W. Green (1964) Several new slip mechanisms in quartz. Trans. Am. Geophys. Union, 45, 103. _______ , D. T. Griggs and N. L. Carter (1964) Experimental evidence of basal slip in quartz. J. Geol., 72, 734-756. Doremus, R. H., B. W. Roberts and D. Turnbull (1958) Growth and Perfection of Crystals. Wiley, New York. Eshelby, J. D. (1953) Screw dislocations in thin rods. J. Appl. Phys., 24, 176-179. Folk. R. L. and J. S. Pittman (1971) Length-slow chalcedony: a new testament for vanished evaporites. J. Sed. Petrol., 41, 1045-1058. Friedlaender, C. (1951) Untersuchung über die Eignung Alpiner Quarze für piezoelektrische Zwecke. Beirr. Geol. Schweiz, Geotechn, Serie, 29, 1-98. Frondel, C. (1936) Twisted crystals of pyrite and smoky quartz. Am. Museum Nat. Hist., Novitates, no. 829. _______ (1962) Silica Minerals, Dana's System of Mineralogy, Vol. 3. Wiley, New York. Geil, P. H. (1963) Polymer Single Crystals. Wiley-Interscience, New York. Gill, A. C. (1893) Beiträge zur Kenntniss des Quarzes. Z. Kristallogr., 22, 97-128. Gomer, R. (1958) Field emission from mercury whiskers. J. Chem. Phys., 28, 457-464. Gross, G. (1972) Zerstörungsfreie statisch-morphologische Untersuchung eines Quarzfundes. Schweiz. Mineral. Petrogr. Mitt., 52, 523-535. Hartman, P. (1973) Crystal Growth. North Holland, Amsterdam., ________ and W. G. Perdok (1955) On the relations between structure and morphology of crystals. Acta Crystallogr., 8, 49-52, 521-524, 525-529. Heritsch, H. (1952) Die Verteilung von Rechts- und Linksquarzen in Schriftgraniten. Tschermaks Mineral. Petrogr. Mitt. 3, 115-125. Holzner, J. (1927) Über die Aufwachsen der Kristalle. Z. Kristallgr., 65, 161-203. Jayaraman, A. (1953) The structure and optical behavior of chalcedony. Proc. Indian Acad. Sci., 38A, 441-449. Johnson, A. (1907) Untersuchungen über Kristallzwillinge und deren Zusammenhang mit anderen Erscheinungen. Neues Jahrb. Mineral., Beil. -Band, 23, 277-344. Jones, F. T. (1952) Iris agate. Am. Mineral., 37, 578-587. Kats, A. (1962) Hydrogen in alpha-quartz. Philips Res. Rep. 17, 133-195. Keith, H. D. and F. J. Padden (1958) Ringed spherulites in polyethylene. J. Polymer Sci., 31, 415-421. ________ and (1959) The optical behavior of spherulites in crystalline polymers. J. Polymer Sci., 39, 101-122, 123-137. Keller, A. (1955) The spherulitic structure of crystalline polymers. J. Polymer Sci., 17, 291-308. _________ (1959) Investigations on banded spherulites. J. Polymer Sci., 39, 151-173. Kozlovskii, M. I. (1962) Spiral growth and dissolution of crystals. In A. V. Shubnikov and N. N. Sheftel, Eds. Growth of Crystals, Vol. 3. Consultants Bureau, New York, 101-106. Lemmlein, G. G. (1936) On twisted quartz. Dokl. Acad. Nauk URSS, 4, 279-282. _______ (1937) Observations on twisted quartz. Izvest. Acad. Nauk URSS, Geol. Ser., 5, 937-964. _______ (1944) The relative number of left- and right-handed quartz crystals. Men. Soc. Russe Mineral., 73, 94-100. ________ (1946) On the growth of quartz on chalcedony. Acad. Sci. URSS, D. S. Belyankin Jubilee Vol., 130-139. Lund, E. H. (1960) Chalcedony and quartz crystals in silicified coral. Am. Mineral., 45, 1304-1307. McLaren, A. C., J. A. Retchford, D. T. Griggs and J. M. Christie (1967) Transmission electron microscope study of Brazil twins and dislocations produced in natural quartz. Phys. Star. Solidus, 19, 631-644. Meyer, O. and S. L. Penfield (1890) Results obtained by etching a sphere and crystals of quartz with hydrofluoric acid. Trans. Conn. Acad. Sci., 8, 158-167. Michel-Lévy, A. and C. P. E. Munier-Chalmas (1892) Memoires sur diverses formes affectees par le reseaux elementaire du quartz. Bull. soc. mineral. fr., 15, 159-190. Miuskov, V. F., L. I. Tsinober and V. Gordienko (1973) Deformation dislocations in natural quartz crystals. Soviet Phys.-Crystallogr., 18, 209-211. Oehler, J. H. (1974) Hydrothermal crystallization of silica gel. Bull. Geol. Soc. Am., 87, 1143-1152. Pelto, C. R. (1956) A study of chalcedony. Am. J. Sci., 254, 32-50. Price, F. P. (1959) The structure of high-polymer spherulites. J. Polymer Sci., 37, 71-89. Raman, C. V. and A. Jayaraman (1953) The structure and optical behavior of iridescent agate. Proc. Indian Acad. Sci., 38A, 199-206. ______ and (1955) On the optical behavior of cryptocrystalline quartz. Proc. Indian Acad, Sci., 41A, 1-6. Reis, Om M. (1916) Einzelheiten Ober Bau und Entstehung von Enhydros, Kalzitachat und Achat. Geognostisch Jahresheft, 29/30, 81-298; 31/32, 1-92 (1918). Riebling, E. F. and W. W. Webb (1957) Some new whiskers. Science, 126, 309. Rosicky, V. (1933) Sur les groupements tordus des cristaux du quartz de Suisse. Spisy Vyd. Prero Fak. Masarykovy Univ., Brno, no. 87, 25-31 (French resume). Sadanaga, R. and M. Bunno (1974) The Wakabayashi Mineral Collection. University of Tokyo Press, Tokyo. Tanford, C. (1973) The Hydrophobic Effect. Wiley-Interscience, New York. Tschermak, G. (1894) Ueber gewundene Bergkrystalle. Denkschr. Akad. Wiss. Wien, Math. Nat. Kl., 61, 365-400. Webb, W. W., R. D. Dragsdorf and W. D. Forgeng (1957) Dislocations in whiskers. Phys. Rev., 108, 498-499. Weiss, C. (1836) Ueber rechts and links gewundene Bergkrystalle. Abh. Akad. Wiss. Berlin, Phys. KI., 187-206. NOTES 1 Mineralogical contribution no. 499 2 A different convention has been used by some authors, in which the seeming
direction of rotation of the terminal prism edge, as seen when the crystal is
viewed along the polar [11 Manuscript received March 15, 1977; accepted for publication August 26, 1977.
|