| Home | AmMin | GMR | RiMG | Collectors Corner | Directory | Short Courses | |
|
|
|||||||

|
|
Volume 42, pages 362-366, 1957 THE GRINDING HARDNESS OF DIAMOND IN A PRINCIPAL CUTTING DIRECTION* REYNOLDS M. DENNING, University of Michigan, Ann Arbor, Michigan. ABSTRACT A series of facets in zone [010] was ground on a diamond. The grinding direction was maintained parallel to the zone axis, and the cutting rates were determined. It is shown that the grinding hardness of diamond even along a principal (four-fold) axis is dependent upon the orientation of the surface on which the measurement is made. It is not possible to represent a grinding hardness solid, analogous, for example, with the optical indicatrix of transparent crystals. The implication is that if it were possible to develop a theory of grinding hardness in diamond, the simplest hardness model must be represented by a tensor of at least fourth order.
The purpose of the present note is to demonstrate that the grinding hardness of diamond, even parallel to a principal (four-fold) axis, is dependent upon the orientation of the surface on which the measurement is made. Grinding hardness is considered reciprocal to the rate of removal of material by grinding. It is fairly easy to demonstrate such a relationship for the more randomly located cutting directions. In the case of a four-fold symmetry axis the relatively easy grinding along such a direction in any plane makes the measurement rather difficult. The preliminary data presented in a previous paper (Denning, 1955) are not sufficiently exact to warrant positive conclusions for so special a direction as the one under consideration. Such uncertainty exists because the measurements were made at widely separated times, which necessitated unavoidable systematic errors in the grinding rate of the reference standard. In that work the hardness data, for various grinding directions on a given surface are consistent with each other, but a comparison of hardness from one surface to another is only approximately valid.
In the present study measurements were made simultaneously on two
diamonds, one ground on (001) along [010] as a reference, the other on a
series of planes in zone [010]. The cutting direction on the latter diamond was
maintained in the [010] direction. The relative grinding hardness was
determined for each of these planes. The relative grinding hardness along
[010] is the same in either direction, since this direction is normal to a
symmetry plane. If, however, the surface on which the measurement is made is not
quite normal to the symmetry plane (010), then an appreciable asymmetry of
grinding rates is introduced. For example, if a plane whose two-circle
coordinates are φ=90°, ρ =1° is ground toward (
The latter three all exhibit about the same hardness as the four analogous
directions on a plane accurately parallel to (001). In practice, at least with the methods here employed, it is impossible to orient planes with an accuracy of much better than 15 minutes of arc. In order to minimize orientation errors the planes studied were oriented to a tolerance of
+0', -30' from parallel to [010]. That is, the orientation error was kept
toward the soft, rather than the hard, direction. In this way a valid
average of cutting rate can be obtained. Such an average could not be
used if the surface were located to ± 15'. The accuracy of the ρ angle is
of no particular importance because of the small rate of change of relative grinding hardness with respect to this angle. Special care has been taken to minimize systematic errors. The areas of the facets have been kept constant to within a factor of two. The shapes of the facets were
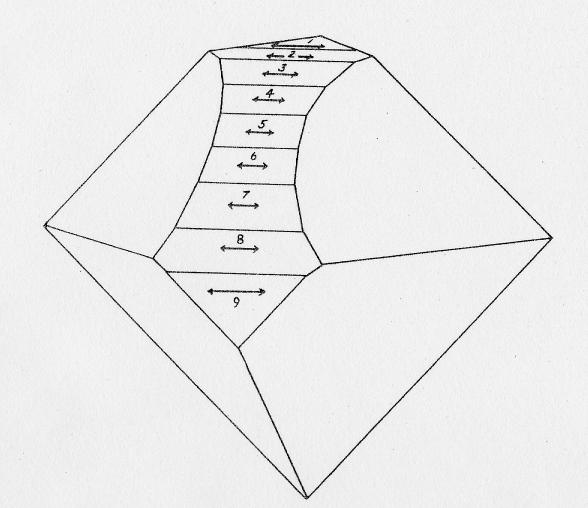
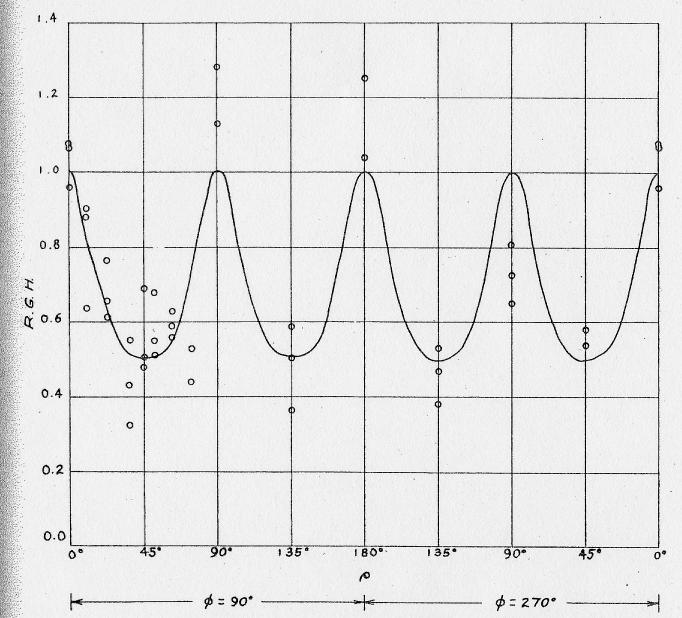
nearly identical in all tests except one. The lowest value of relative grinding hardness was determined on (00 Table 1 is a summary of the data obtained from 14 facets. Each hardness value is the average of three independent determinations. The last column is an average of the four quadrants according to the symmetry and adjusted to unit hardness for the reference direction. Figure 1 shows the appearance of an octahedron on which the first nine facets of Table 1 are drawn. The length of the arrows is proportional to the relative grinding hardness in the direction of the arrows. In Fig. 2 the dependence of hardness along [010] for the series of planes is given. The curve is idealized, but the original data points are included. The validity of averaging these quadrants has been established from other measurements which involve a greater hardness variation than those under consideration (Wilks & Wilks, 1954; Denning, 1955). A statistical examination of the data removes any doubt of the reality of the difference in relative grinding hardness on the optimum grinding direction of the cube and dodecahedron. The optimum cutting direction on the dodecahedron is slightly softer than the same direction on a cube facet. The magnitude of the observed hardness variation is not very great. To the practical cutter or user of diamonds, the hardness variation along a four-fold symmetry axis is negligible. Such variation may be of theoretical interest in the detailed interpretation of the relation of the diamond structure to directional hardness variation.
TABLE 1. RELATIVE GRINDING OF HARDNESS OF DIAMOND ALONG [010] ON A SERIES OF LINES. (THE SECOND DECIMAL PLACE IS NOT SIGNIFICANT)
It is of interest to note that to specify fully the continuous grinding hardness values of a crystal, the hardness values must be plotted against three dimensions. Two of these may designate the orientation of the grinding direction (or plane being ground) and the third, the position of the plane on which measurements are made (or azimuth of grinding direction on the plane). For this reason it is not possible to construct a grinding hardness solid, analogous, for example, with the optical indicatrix of transparent crystals. The implication is that if it were possible to develop a theory of grinding hardness in diamond, the simplest hardness model must be represented by a tensor of at least fourth order. It might seem that since a factor of two of hardness variation is not very great, that such a refinement is needed only if the higher order effects are to be explained. As more general directions are studied, the dependence of hardness in a given direction upon plane orientation is strikingly large. Actually such a relationship is implicit in the results of the hardness measurements in various azimuths on selected planes. The writer acknowledges his thanks to Mr. Donald Hausen, who painstakingly made the hardness measurements. This investigation was supported by the Crystal Hardness project of the Office of Naval Research. The diamonds were contributed by Industrial Distributors, Ltd., of Johannesburg. REFERENCES DENNING, R. M. Directional grinding hardness in diamond: A further study: Am. Mineral., 40, 186-191 (1955). WILKS, E. M., AND WILKS, J. The hardness properties of cube faces of diamond: Phil. Mag. ser. 7, 45, 844- 849 (1954). Manuscript received Oct. 22, 1956. NOTE Contribution from the Department of Mineralogy and Petrography, University of Michigan, No. 213.
|