| Home | AmMin | GMR | RiMG | Collectors Corner | Directory | Short Courses | |
|
|
|||||||

|
|
Volume 34, pages 142-162, 1949 THE FREQUENCY OF TWIN TYPES IN QUARTZ CRYSTALS1 H. R. GAULT, Lehigh University, Bethlehem, Pa. CONTENTS
Abstract 142 ABSTRACT The frequency of twin types and the handedness were determined for 1,179 crystals from six localities by the use of etch figures developed with hydrofluoric acid. It is shown that. twinned quartz crystals are much more common than untwinned and that the frequencies of twin types and the ratios between twin types vary from locality to locality. It is suggested that crystals twinned according to both the Dauphiné and Brazil laws should be called "Dauphiné-Brazil" twins rather than by the names that have been previously applied. The local variations of twin ratios are thought to be a reflection of geologic environment. INTRODUCTION Some years ago while engaged in etch-figure work with the late Dr. A. P. Honess, it became desirable to etch and study a few low-quartz crystals from two localities. The crystals from the first locality showed considerably more twinning than those from the second, although the unetched crystals gave no indication of any twinning. A search through the literature disclosed many articles on twinning in quartz but there were few statistical data on the frequency distribution of twin types and of right- and left-handed crystals. Further studies were made on additional crystals from these two localities and from four others in order to determine the frequency of twin types for each locality and the frequency of right- and left-handed quartz crystals. Interest in this problem arose more from the geological implications than from the purely mineralogical aspects. The writer is indebted to the late Arthur P. Honess for an introduction to the etch method and for encouragement in this study. Thanks are extended to several former associates for gifts of certain crystals and for opportunities to discuss the problem. C. Wroe Wolfe kindly loaned his translation of Friedel's Lecons de Cristallographie and Siemon Muller certain Russian translations. Appreciation is expressed to J. D. H. Donnay, D. M. Fraser, C. S. Hurlbut, Jr., Earl Ingerson, and R. B. Sosman for constructive criticism of the original manuscript, and to R. D. Butler for discussions about the phantom crystals. J. C. Wynn very kindly loaned his drawings of phantom crystals from Brazil. There is a voluminous literature on quartz but it is beyond the scope of this paper to review all of it. Many of the references are concerned with descriptions and study of quartz twins and twinning, the nature of the twin boundaries, quartz etch figures, vicinal faces, relations of form and twinning to temperature of formation, as well as geology and occurrence. Among the many workers who prior to 1940 contributed to the study of quartz along these lines are Baumhauer, Bendrich, Bomer, Bond, Brauns, Des Cloiseaux, Drugman, Friedel, Gaudefroy, Gill, Goldschmidt, Heide, Hirschwald, Ichikawa, Kalb, Larsen, Leydolt, Martini, Meen, Meyer, Molengraaf, Mügge, Nacken, Niggli, Penfield, Rose, Sosman, Trommsdorf, Von Roth, Websky, Weiss, Wright, and Witteborg. Since 1940, because of the great war demand for quartz oscillator-plates in the radio industry, added impetus was given in the United States to the study of quartz and its twinning by the work of Armstrong, Bond, Frondel, Gordon, Hurlbut, Parrish, Stoiber, Willard, and others. No attempt will be made to cite all of the references; some are noted in recent papers by Frondel, Parrish, Hurlbut, Gordon and others. Heide (1928) tabulates data for twenty-eight twin halves of Japanese twins from Saubach giving three with no twinning, fifteen twinned after the Dauphiné law, of which seven were left-handed and eight were right-handed, two after the Brazil law and eight after the Dauphiné-Brazil law. Trommsdorf (1937) examined 4,483 crystals from Villa Cristallina near Tres Capone, Brazil, and reported that 0.91 per cent were twinned according to the Brazil law. He also found that about half of those examined were right-handed and half were left-handed. His results are markedly at variance with those of Hurlbut (1946) for Brazilian quartz.
Thompson (1937) used the positions and striae on the s {11 Saparova (1938) reported that, of thirty crystals from Wermsdorf, nineteen were twinned; eighteen according to the Dauphiné law and one according to the Brazil law. Hurlbut (1946) gives some excellent data on the volume percentages of Dauphiné and Brazil twinning in quartz crystals from thirteen localities in Brazil, two in Guatemala, and one in Colombia. His article is based on research to determine which localities would yield the best grade of oscillator-plate quartz. Hurlbut examined 52,000 wafers cut from 3,015 crystals and thus gives a quantitative viewpoint not ordinarily obtainable by those outside the quartz industry. Since he did not report the frequencies of twin types or twinned and untwinned crystals, his data cannot be directly compared with those presented below but there seem to be some relationships. Hurlbut's data (p. 449, Table 3) shows differences in the volume percentages of twinning with greater differences among Brazilian, Colombian, and Guatemalan localities than among just Brazilian localities. This is brought out more strikingly by the yield of oscillator-plate blanks per pound than by the percentages of twinning, although, as Hurlbut points out, it is unfair in generalizing to say that Colombian and Guatemalan quartz are of lower grade (and thus in one sense more strongly twinned) than Brazilian quartz because of the limited quantities studied from the former localities. There is also quantitative information on high-quartz crystals. One of the more informative studies is Mügge's (1892) on pyrogenic or rock forming quartz including a number of euhedral high-quartz crystals from porphyries. QUARTZ ETCH FIGURES Excellent discussions of etch figures of quartz are given by Leydolt, Mügge, Ichikawa, Nacken, Gill, Meyer, Penfield, and Bond. Honess (1927) has discussed the entire subject of etching very thoroughly. It is relatively easy to distinguish between right- and left-handed quartz by the use of etch figures (Meyer and Penfield, 1889) and, further more, the etch figures for all faces of one form etched with the same solvent are quite distinctive from those of other forms. The fact that different solvents develop different etch figures on the same face is of no significance here. Quartz can be etched by several solvents. Hydrofluoric acid has been the most widely
used, although the quartz industry now uses a water solution of ammonium
bifluoride (Parrish and Gordon, 1945) for safety reasons. Hydrofluoric acid was
used in the present study. The etch figures produced by
hydrofluoric acid on the rhombohedral faces r {10 QUARTZ TWIN LAWS There are six known twin laws for low-quartz (Friedel, 1926), namely, Dauphiné, Brazil, Japanese, Esterel, Sardinian, and Breithaupt. In addition, there is a complex type of twinning which is a combination of the Dauphiné and Brazil laws and has been variously called. Liebisch twinning, combined twinning, combined optical twinning, combined Dauphiné-Brazil twinning, and Dauphiné-Brazil twinning. Dauphiné, Brazil, and Dauphiné-Brazil twins are penetration twins and are the most common types. Although they are the only twin laws considered in this study, a summary of all the known twin laws of quartz is included. SUMMARY OF TWIN LAWS OF QUARTZ
1 Heide (1928) considers four "laws" for Japanese twins of which the
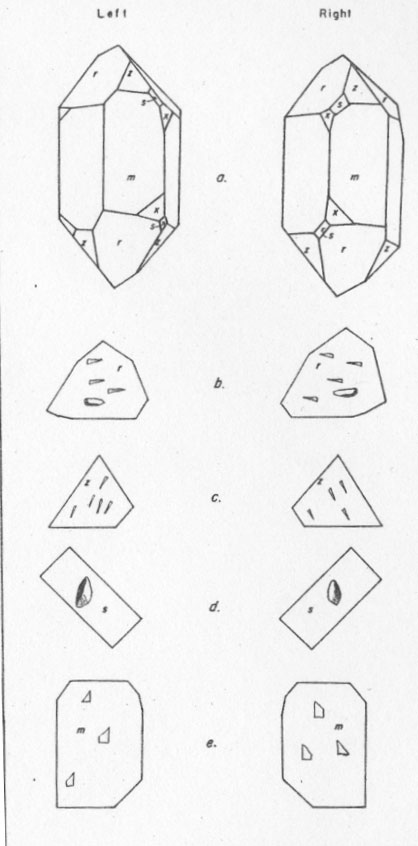
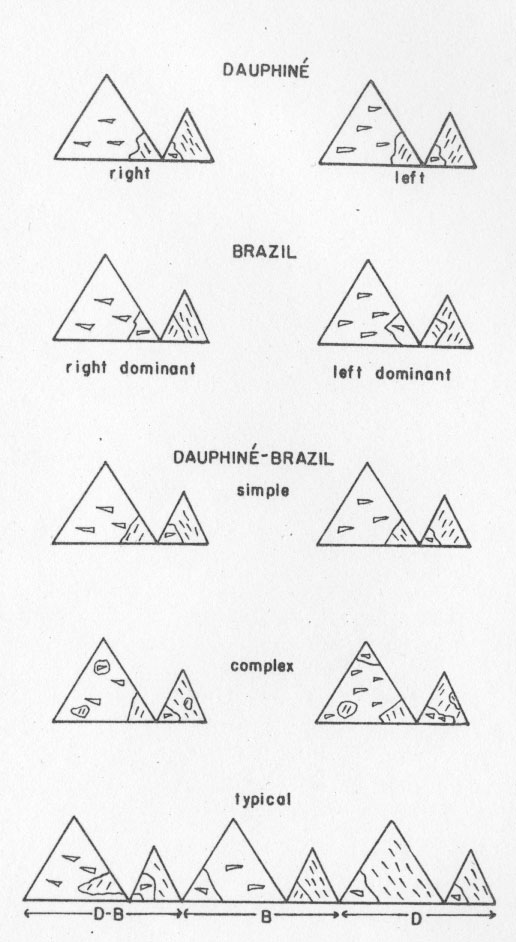
common designation (11 Recognition of penetration twins is largely a matter of etching any observing the type and arrangement of the etch figures (Fig. 2). It is generally accepted that untwinned quartz is relatively uncommon and that most crystals are twinned according to the Dauphiné law and the Brazil law (Booth and Sayers, 1939; Gordon, 1945; and others); Booth and Sayers also indicate that Dauphiné-Brazil ("combined") twinning is very common.
In Dauphins twinning, the r {10
Brazil twinning, also known as chiral or optical twinning, is the result of an
intergrowth of a right- and a left-handed individual as if there had been a
reflection across a second order prism. Thus a right r {10 Internal twin boundaries of Dauphiné and Brazil twins in sections through the crystals are well illustrated and described by many workers in recent years by Frondel (1945), Gordon (1945), Johnston and Butler (1946), Parrish and Gordon. (1945), Willard (1944) and others. The Dauphiné-Brazil twin has been described for many years but does not seem to have acquired a name until recently. Leydolt (1855, pl. 4) gives an excellent illustration of this type of twinning in a basal section. Liebisch (1896) mentions it as one possible type of twin but applies no name. Lewis (1899) describes it as a possible composite crystal ("laevo-dextrogyral twins β") and refers to amethyst crystals which supposedly show it. This complex twinning is pointed out in both editions of Weiss, Mineralogy (1902, 1929) and by Klockman (1923). Heide (1928) refers to Liebisch's description and shows the symmetry of the twinned crystals schematically with etch-figure patterns. Heide's discussion is one of the most complete. Gaudefroy (1933) also recognized this type of twinning. No mention of twinning of this type is made in Hintze's Handbuch, in the 6th Edition of Dana's System of Mineralogy (1892), Zirkel's Elemente der Mineralogie (1897), nor in Tutton's Crystallography (1922). The first name applied to this twinning was apparently given by Ivanov and Shafranovsky (1938) who illustrate types of twinned crystals which they refer to as simple and complex Liebisch twins. Booth and Sayers (1939) describe and figure this same type of twinning but suggested the name "combined optical twinning." Willard (1944) also describes and figures such twinning and calls it "combined twinning." Thomas (1945) suggested "combined twinning" as a shorter form of "combined optical twinning." Gordon (1945) and Frondel (1945) have also used the term "combined twinning" as have a few others. According to the illustration of Ivanov and Shafranovsky (1938), a simple Liebisch twin is a rigidly defined combination of both Dauphins and Brazil twin-law effects in such a way that there is first an apparent rotation about the c axis (Dauphiné effect) and then there is an apparent reflection across a second order prism face (Brazil law effect). Thus in this simple twin a right r and a left z face become coincident (see Fig. 2) rather than a right r and a left r as in a Brazil twin or a right r and a right z as in a Dauphins twin. Descriptions and figures by Heide (1928) and the comments of others agree in principle with the above. 'This combination of the Dauphiné and Brazil laws is perhaps analogous to the complex albite-Carlsbad twin in the triclinic feldspars. There is, however, one difference. Because quartz is enantiomorphous, the twining action cannot be performed by a single operation as it can for the albite-Carlsbad twin. In the albite-Carlsbad twin the simplest form has only two parts (1 and 2' of Winchell, 1933); part 1 is in the original position and part 2' is in a position that can be obtained by two rotations, or corresponding to the albite law and one to the Carlsbad law. Similarly in the simple Dauphiné-Brazil twin there are two parts, one in the original position and the second obtained by a rotation combined with a reflection. Such dual Dauphiné-Brazil twins are uncommon in quartz. In most crystals twinned according to the complex Dauphiné-Brazil law, as observed in the present study, there are many parts so that any one part will have a Dauphiné twin relation to a second, a Brazil twin relation to a third, a Dauphiné-Brazil relation to a fourth. Typical Dauphiné-Brazil twin-law etch-figure patterns on the rhombohedral faces are shown in Fig. 2, which illustrates possible etch-figure patterns on rhombohedral faces where the Dauphiné effect appears on one face, the Brazil effect on a second face, and the Liebisch effect on a third face. Some of these variations have been noted. On the basis of date of publication, Ivanov and Shafranovsky's name "Liebisch" should have precedence over the others. From the standpoint of usage, the term "combined twinning" seems well established and understood in the quartz oscillator-plate industry. Despite precedence and usage, it is suggested that this type of twinning in quartz should be called "Dauphiné-Brazil twinning" just as the complex feldspar twin laws are named after their combinations. As crystals showing only a simple Dauphiné-Brazil twin pattern or "Liebisch" effect are rare, it may be desirable to drop the term "Liebisch."PROCEDURE All of the crystals used in this study possessed the trigonal symmetry of low-quartz. Groups of crystals were obtained from each locality without any selective sampling other than the requirement that each crystal have its terminal faces completely developed. The crystals were etched with hydrofluoric acid until the etch figures were sufficiently mature for recognition of outline and orientation. No attempt was made to control the time of etching or the concentration of the acid. After etching, the crystals were examined under a binocular microscope in reflected light and classified according to the twin laws indicated by the etch figure patterns (see Fig. 2).
All observations were confined to the rhombohedral faces of crystals except in the case of those from Herkimer County, N. Y. This was necessary in most cases because of the lack of development of prism faces or because the prism faces were too striated or otherwise roughened for etching. In some cases, particularly with the Arkansas crystals, it was possible to trace twin boundaries from the rhombohedral faces to the adjacent prism faces. RESULTS AND DESCRIPTION OF MATERIAL A total of 1,179 crystals from six widely separated geographic locations and distinct geologic occurrences were examined. The statistical data are presented in Table 2. No distinction is made in the table between simple and complex Dauphiné-Brazil twinning. In classifying Brazil and Dauphiné-Brazil twins there is always the problem of whether they should be placed with right-handed or left-handed crystals. Only in few instances was any difficulty experienced in determining which type of quartz was dominant in a crystal. It is generally obvious from visual inspection that one or the other is dominant. As others have pointed out, right- and left-handed quartz occur in about equal proportions in "untwinned" crystals as well as in Dauphiné twins. Brazil twins and Dauphiné-Brazil twins, with respect to to dominant handedness in each crystal, also show right- and left-handed quartz in about equal proportions. The relative frequency of untwinned and twinned crystals varies from place to place, and the relative frequency of the interpenetration laws also varies considerably. Accordingly, there is a determinable ratio between twin types for individual localities. For the total number of crystals studied, Dauphiné-Brazil twins are slightly more common than Dauphiné twins. Brazil twins are relatively uncommon. However, in the breakdown by localities, the relative frequencies, at any one occurrence show more variation. Actually, Dauphiné twins are more abundant in four of the six occurrences (Arkansas, Utah, Maryland, Alaska) than Dauphiné-Brazil twins. Brazil twins are more abundant than Dauphiné twins and nearly equal to Dauphiné-Brazil twins at one locality (New York). Dauphiné twins are present at all localities but Brazil twins are lacking at three localities (Pennsylvania, Maryland, Alaska). Dauphiné-Brazil twins were not recognized at two localities (Utah and Maryland).
An apparent correlation was noted, particularly for the Arkansas crystals,
between the frequency and amount of twinning and the shape of the crystal. The
more tapered crystals (candle-like habit) tend to show less twinning. Hurlbut
(1946) shows this quantitatively in graphic form for Brazilian quartz. There is
also a suggestion that individual crystals bearing the less common faces s
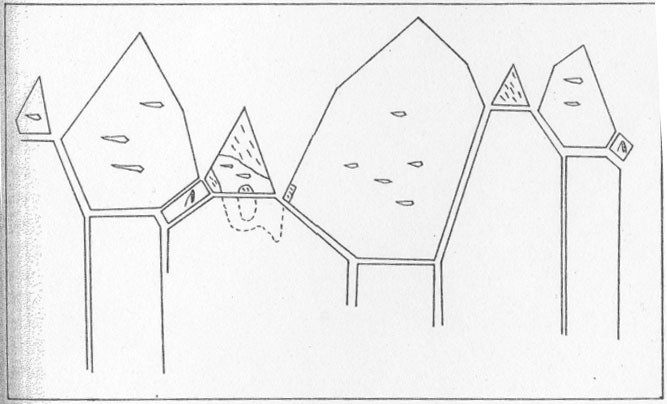
{11 Arkansas crystals - Quartz crystals from Arkansas are well known and. their occurrence and geology have been well described by Miser (1943) and Engel (1946). The material used in this study came from the Fisher mines about seven miles southeast of Mount Ida, Montgomery County, near the southwest end of the main district in western Arkansas (Engel Fig. 1, 1946). The crystals are singly terminated and range from 3/8 inch to one inch in diameter and one inch to two inches in length. They belong to Engel's simple type (p. 606, 1946). Most of them have clear terminations with milky lower portions. None of the crystals reported in Table 1 showed any s or x faces. Typical twin boundaries on the rhombohedral faces of the Arkansas crystals are shown in Fig. 3.
In addition to the Arkansas crystals reported in the table, a second group of
160 singly terminated crystals representing a number of Arkansas localities were
also examined. It is a pleasure to thank Mr. Hugh D. Miser, U. S. Geological
Survey, for the gift of these crystals. The crystals in this group are
distinctive in that they all show the development of at least one x {51 TABLE 1. FREQUENCY OF TWIN LAWS IN ARKANSAS QUARTZ CRYSTALS
Ratio (d:b:db) 10:7.5:3 *R=right; L=left; nt=no twinning; d=Dauphiné; b=Brazil; db=Dauphiné-Brazil.
This assemblage of crystals shows a greater proportion of untwinned crystals than do those lacking the x and s faces. This difference is largely at the expense of the Dauphiné twins. There is also a slight decrease in the total frequency of intergrowths of right- and left-handed individuals with the Dauphiné-Brazil twinning giving way to Brazil twinning. Pennsylvania crystals. -- There are a number of localities in Pennsylvania and Maryland where quartz crystals occur in soil overlying limestones. Presumably they are residual from the weathering of the limestones. The material described here came from a field underlain by Trenton limestone (Butts and Moore, 1936) just east of Lemont, Centre County. Quartz crystals were found also in the limestone and in calcite veins cutting the limestone. None of them, however, was as large as the largest crystals found in the soil. TABLE 2. FREQUENCY OF TWIN LAWS IN QUARTZ CRYSTALS
Total right-handedd or right-handed dominant 518 or 51.6% * R=right; L=left; nt=no twinning; d=Dauphiné; b=Brazil; db=Dauphiné-Brazil. 1 12 additional crystals showed Rb at one end and Lb at the other. 3 additional crystals showed Rnt at one end and Lnt at the other end. 2 1 addition at crystal showed Rnt at one end and Lnt at the other end.
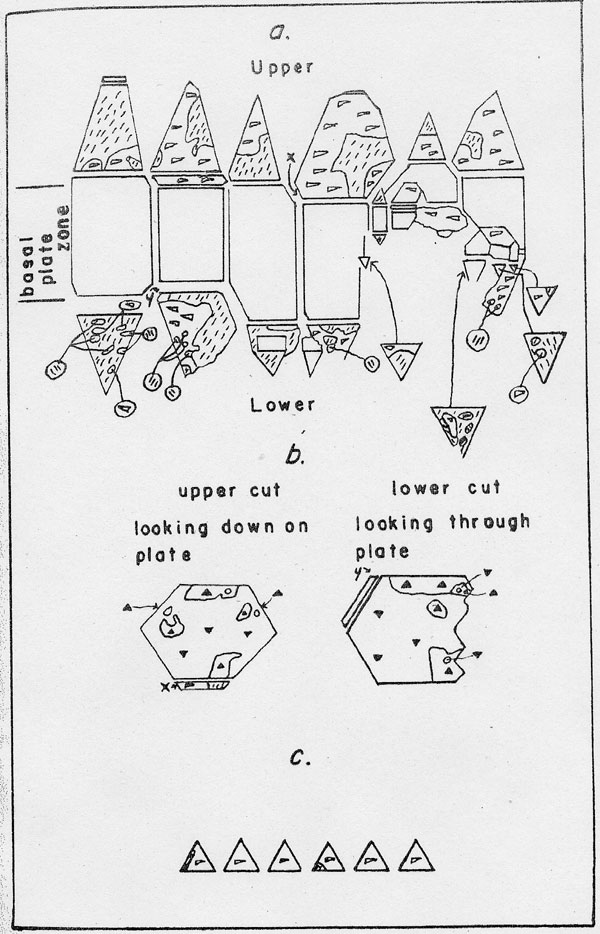
All of the crystals studied are doubly terminated with roughened striated prism faces. Inclusions of dark materials, cavities, irregular growth habits and internal flaws are common to all crystals. They are not clear like the Herkimer County, New York, crystals. The crystals examined are one-quarter inch to one inch in diameter and one-half inch to one and one-half inches long. Typical twin boundaries on the rhombohedral faces are shown in Fig. 4a. Figure 4b shows internal twinned parts. Utah crystals -- The crystals were taken from a small drusy specimen collected in the Tintic district. Barite crystals were associated with the quartz crystals. The latter are small singly terminated crystals with a diameter of about one-eighth inch and a length of about three-eighth inch. New York Crystals --- The material used in this study is typical of the well-known Herkimer County, New York, product. The crystals range from one-quarter inch to three-quarters inch in diameter and one-half inch to one and one-half inches in length. On all of these crystals it was possible to trace the external twin boundaries on the prism faces. The exact locality is unknown, but all are from the same general location. Maryland crystals -- These crystals came from a small quartz vein in the Wissahickon formation near Baltimore. The crystals are about the same size as the Tintic, Utah, material and are singly terminated with only the rhombohedral faces developed.Alaska crystals - The Alaska crystals are from Glacier Basin, near Wrangell, Alaska. They occurred as drusy deposits with a comb-like structure in vugs or along the walls of quartz-fluorite breccia veins cutting a series of metamorphic rocks in the Coast Ranges. The geology and veins are described by Gault, Rossuran and Flint (1944a & b). The crystals are singly terminated with only the rhombohedral faces developed. The bases of the terminations are one-eighth inch to one-half inch in diameter. Typical twin patterns are shown in Fig. 4c.
The etch figures on these crystals indicate an unusual development of the r {10 No crystals were noted twinned only according to the Brazil law. In the crystals twinned according to the Dauphiné-Brazil complex law, the second enantiomorphous individual always made its appearance near the base of the rhombohedral faces and in practically all cases it was indicated by the coincidence of right- and left-handed r faces. DISCUSSION Some discussion of the procedure seems warranted to avoid criticism with regard to confining observations to the rhombohedral faces. It is obvious, of course, that where no prism faces were developed, no etch figures could be obtained for studying twin boundaries on the exterior of the crystals. Some twinning may have been overlooked by not studying the prism faces as thoroughly as the rhombohedral faces. However, further observations were made, where possible, on those crystals which showed no twinning on the rhombohedral faces to see if there were twin boundaries on the prism faces not extending to the rhombohedral faces. In some instances such boundaries were observed but not in enough cases to change noticeably the actual numbers of crystals and, even less, to change the ratios among twin types. Another comment which may be made is that this study has dealt thus far only with the exterior of the crystal and no consideration has been given to the interior. An approach to this question of interior twinning was made by taking 20 Arkansas crystals which showed no twin boundaries on the rhombohedral faces, cutting a basal section from each one slightly below the base of the termination, and etching the basal sections. Of the 20 sections, 12 showed no twinning at all. The other 8 crystals showed quite small irregular patches of twinning which were restricted to the very edges of the crystals but were not always recognizable on the prism faces. Four of these eight crystals each carried one small twinned part near the center of the section. Because these did not appear on the rhombohedral faces, it is suggested that some twinned parts were wholly internal, i.e. entirely surrounded by other quartz. Heide (1928) also suggested that material appearing as untwinned quartz in poorly developed crystals might actually be twinned elsewhere in the crystal. This suggestion is further substantiated by Hurlbut, 4 who, from his extensive experience in the quartz industry, says it is quite possible, and frequently happens that twinned parts are entirely enclosed by other quartz and do not appear on the exterior of the crystal. Hurlbut's work with so many thousands of wafers should be conclusive.
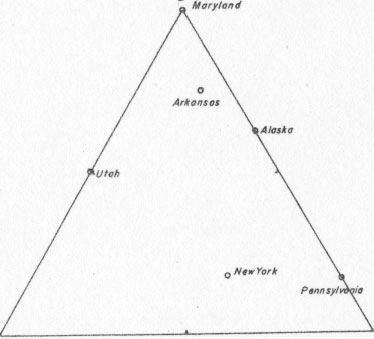
Of the 20 crystals mentioned above, 40 per cent of those tested showed twinned parts which were not recognized on the rhombohedral faces. Although this is a considerable percentage of the so-called untwinned crystals, actually the distribution of these twins did not change the ratio of twin types. Thus, if there is any hesitancy in accepting the untwinned group as truly untwinned crystals, it can be disregarded and only the ratios of twin types accepted. On this basis, the approximate ratios of twin types for each locality are given below as derived from the relative frequencies in Table 2 (see also Fig. 5). Practically, of course, the study of twin boundaries in quartz only at the surface of the crystals does not tell much about the extent of the twinned material within the crystal. Confining the observations to the rhombohedral faces limits this still more. However, it can be shown from the geometry of most of the crystals that the principal direction of growth was parallel to the c axis and probably on the rhombohedral faces. It is readily apparent that if, as a seed crystal grows, the rhomb faces are the areas of greatest deposition the crystal will become elongate parallel to the c axis. In order to produce broad short crystals the rate of growth on the prism faces must be greater than on the rhomb faces. One indication of direction of growth is phantom crystals. Johnston and Butler (1946) figure a number of phantom crystals from Brazil and state (p, 639): The prismatic habit of quartz is reflected by the phantom relations - growth was usually pronounced along the c axis after formation of the phantom even though the center of gravity in the basal planes conspicuously shifted. Their figures as well as other unpublished figures 5 of phantom crystals from Brazil all show the rhomb faces as having a greater thickness of quartz in each phantom than do the corresponding prism faces.6In a general way, similar conditions of growth are inferred for the crystals described herein, all of which have their long dimension parallel to the c axis. Therefore, observations on the rhombohedral faces of these crystals should reflect the frequency and nature of twinning at the places of greatest deposition, at least during the last stage of growth of the crystals. The groups of so-called untwinned crystals should now take on more significance because they would indicate there was no twinning developing at that time. Unless there were radical changes in conditions of growth from early to late stages, the observations should perhaps be an indication of what would be found within the crystal. Even if there were radical changes from early to late stages, it seems reasonable to believe that they would have been in degree of controlling factors rather than in type. Where no twinning or only isolated patches of twinned quartz are exposed at the surface of the crystal, it does not seem probable that the interior of the crystal should show strong twinning with many parts.
RATIOS OF TWIN TYPES
Because internal twinned parts are not taken into account, these data are not rigidly quantitative but rather they express a relative frequency of and ratio between twin types. If the materials described herein were studied along the lines applied by Hurlbut (1946), there might be no groups of untwinned crystals but such groups according to the present classification might show only very small volume percentages of twinned quartz.The ratios between twin types for each locality may be characteristic of different types of geologic occurrence. Frondel (1945) has stated that the relative development of Dauphiné and Brazil twinning varies widely as does the individual percentage of the twin types and that the type of occurrence seems to be a controlling factor in the relative development of twins. Hurlbut's (1946) data, although given as volume percentages indicate a difference in the amount of twinning from place to place. As Hurlbut points out, the correlation between percentage of twinning and yield of oscillator blanks per pound is far from perfect, but study of his data shows the yield from Brazilian localities to fall within certain limits which are higher than the limits of the yield from other than Brazilian localities. The correlation of volume percentages of Dauphiné and Brazil twinned parts with locality is less obvious than for yield of blanks, but again all of the Brazilian localities fall within certain limits outside of which the volume percentages of the other localities lie. There is also a suggestion, albeit weak, that for a group of localities of similar origin there may be upper and lower limits for the volume percentage of twinning as compared with other types of occurrences. Unfortunately, Hurlbut could not list specific localities for security reasons, and so it is not possible to compare his Brazilian localities with the four major quartz belts in Brazil (Stoiber, Tolman, and Butler, 1945). Possibly a closer correlation and narrower limits for each belt might be forthcoming. On the other hand, Campbell (1946) includes two of the quartz belts described by Stoiber in one type of geologic occurrence. It would appear that very broadly speaking all Brazilian localities are similar in origin and geologic occurrence and belong to a single genetic period (Kerr and Ericksen, 1942; Johnston and Butler, 1946, and others). Where the frequencies of twin types for a number of localities fall within certain limits, these limits may be distinctive for deposits which have similar conditions of origin and geologic environment, but which are geographically distinct. Further study is needed to verify or refute this. Engel states (p. 608, 1946) that, although all correlation of occurrence and nature of optical twinning is speculative, it is known that the ratio of highly twinned to relatively untwinned quartz is fairly constant for a single deposit or group of related deposits. It varies considerably between localities in dissimilar country rock. The problem of the geological significance of variations of the frequency of twins and of the ratios between twin types is of considerable interest, but many additional observations and some experimental data are needed before any satisfactory conclusions can be drawn. The frequencies of twins and the ratios between twin types seem to be a reflection of the mode of occurrence which will require the consideration of many environmental factors, in fact, more than can be resolved at present. Thus it is not possible to relate twin ratios and frequencies at this time to geological occurrence. Factors which probably exert an important influence are temperature, concentration, impurities, nature of the wall rock, rate of cooling and pressure. Temperature studies have been made to (1) determine whether the quartz crystallized as the high or low form (Mügge, 1907, 1921; Wright and Larsen, 1909) and (2) to distinguish temperature stages in types of low-quartz crystals (Maucher, 1914; Mügge, 1921; Kalb, 1933, 1935; Virovlyanski, 1938a, 1938b). The criteria of the nature of twin boundaries and their patterns for determining high- or low-quartz crystallization are becoming less and less applicable as a result of recent work (Frondel, 1945; Armstrong, 1946). Virovlyanski (1938a and b) and Engel (1946) found Kalb's scheme (based on vicinal faces) unreliable. The influence of impurities on twinning in quartz has been pointed out recently by Zinserling (1941), Johnston and Butler (1946), and Armstrong (1946). Two types of impurities are important; those incorporated in the crystals during its growth and those which settled out of suspension onto earlier growth planes. SUMMARY AND CONCLUSIONS There is a great need for further observation and experimentation before the geological significance of the frequency of twins and the ratios between twin types in quartz can be fully understood. Temperature measurements on inclusions similar to those reported by Newhouse (1933), Ingerson (1947), and Twenhofel (1947) would be very valuable. Further studies along that line are in progress for the crystals described herein. Study of growth patterns and twinning in the various parts of phantom crystals may contribute much to the problem. There are, however, several well established points with respect to quartz twinning which can serve as a basis for future work. 1 Twinned quartz crystals are much more common than untwinned crystals - in fact, untwinned crystals may be considered a rarity. 2. Penetration twins are the most common type. Contact twins are rare. 3. Crystals twinned according to both the Dauphiné and the Brazil laws should he called "Dauphiné-Brazil" twins rather than "combined" twins. 4. Of the three types of penetration twins, those twinned according to the Dauphiné and Dauphiné-Brazil laws are as a rule more abundant than Brazil twins, particularly the Dauphiné-Brazil. The excess is sometimes slight, sometimes overwhelming. The common occurrence of Dauphiné-Brazil twins has not been fully recognized. 5. Right- and left-handed quartz crystals are found to occur in equal proportions when a sufficient quantity of material is examined. Even in Brazil and Dauphiné-Brazil twins, though one handedness is dominant over the other in each crystal, those with right dominant are equal to those with left dominant. 6. Dauphiné twin boundaries are irregular, whereas Brazil boundaries are more likely to be parallel to crystallographic planes. 7. Crystals on which the less common faces of general forms are developed show less twinning than other crystals from the same locality. 8. The relative frequency of the twin types varies considerably from locality to locality. These variations must surely be a reflection of the conditions of growth and geologic environment. REFERENCES 1. ARMSTRONG, ELIZABETH, (1946), Relation between secondary Dauphiné twinning and. irradiation-coloring in quartz: Am. Mineral., 31, 456-462. 2. BANDY, .MARK C. (1942), Direction of flow of mineralizing solutions: Ec. Geol., 37,330- 333. 3. BOOTH, C. F., AND SAYERS, C. F., (1939), The production of quartz resonators for the London-Birmingham coaxial cable system: P. O. Elec. Eng. Jour., 31, 245-253. 4. BUTTS, CHARLES, AND MOORE, ELWOOD S., (1936), Geology and mineral resources of the Bellefonte quadrangle, Pa.: U. S. Geol. Surv., Bull. 855. 5. CAMPBELL, D. F., (1946), Quartz crystal deposits in the state of Goiaz, Brazil: Ec. Geol., 41, 773-800. 6. ENGEL, A. E. J., (1946), The quartz crystals of western Arkansas: Ec. Geol., 41, 598- 619. 7. FRIEDEL, GEORGES, (1926), Leçons de cristallographie: Berger-Levrault, Paris, 602pp. 8. FRONDEL, CLIFFORD, (1945), Secondary Dauphiné twinning in quartz: Am. Min 30, 447-461. 9. GAULT, H.. R., (1944a), Zinc deposits of Groundhog Basin, Wrangell district, southeastern, Alaska; mimeographed report. U. S. Geol. Surv., (March). 10. _____ ROSSMAN, D. L., AND FLINT, G. M., JR., (1944b), Geology and mineral deposits of Glacier Basin and vicinity, Wrangell district, southeastern, Alaska: mimeographed report, U. S. Geol. Surv., (May). 11. GAUDEFROY, M. C. (1933), Sur les groupements de cristaux de quartz ä axes paralleles Bull. Soc. Min. (France), 56, 5-63. 12. GORDON S. G., (1945), The inspection and grading of quartz: Am. Mineral., 30, 269- 119 13. HEIDE, F., (1928), Die Japaner Zwillinge des Quarzes und ihr Auftreten in Quarz porphyr vom Saubach i. V.: Zeit. Krist., 66, 239-282. 14. HONESS, A. P., (1927), The nature, origin, and interpretation of the etch figure: John Wiley and Sons, New York. 15. HURLBUT, CORNELIUS S., JR., (1946), Influence of twinning on the usability of quartz: Am. Mineral., 31, 443-455. 16. INGERSON, EARL, (1947), Liquid inclusions in geologic thermometry, Am. Mineral., 32, 375-388. 17. IVANOV, N. A., AND SHAFRANOVSKY, I. I., (1938), Outward indications of the important twins of quartz: Soc. Russe Miner., Mem. 67, Iv. 3, 435-445. 18. JOHNSTON, W. D., JR., AND BUTLER, R. D., (1946), Quartz crystal in Brazil: Bull. Geol. Soc. Am., 57, 601-650. 19. KALB, G., (1933, 1935), Beiträge zur Kristallmorphologie des Quarzes: Zeit. Krist. 86, 439-465; 90, 163-186. 20. KERR, P. F., AND ERICHSEN, A. I., (1943), Origin of the quartz deposits at Fazenda Pacú, Brazil: Am. Mineral., 27, 487-499. 21. KLOCKMAN, F., (1923), Lehrbuch der Mineralogie: Stuttgart. 22. LEWIS, W. J., (1899), A Treatise on Crystallography: Cambridge Univ. Press. 23. LEYDOLT, FRANZ, (1855), Ueber eine neue Methode, die Structur und Zusammen setzung der Krystalle zu untersuchen, mit besonderer Berücksichtigung der Varietäten des rhomboedrischer Quarzes: Akad. d. Wiss. Wien, 15, 59-82. 24, LIEBISCH, THEODOR, (1896), Grundr. phys. Kristallographie; Leipzig. 25. RAUCHER, W., (1914), Die Bildungsreihe der Mineralien als Unterlage für die Einteilung der Erzlagerstätten: Freiberg i. S. 26. MEYER, O., AND PENFIELD, S. L., (1889), Results obtained by etching a sphere and crystals of quartz with hydrofluoric acid: Trans. Conn. Acad., 8, 158-165. 27. MIERS, H. A., (1902, 1929), Mineralogy; first edition, London; second edition, London. 28. MISER, HUGH D., (1943), Quartz veins in the Ouachita mountains of Arkansas and Oklahoma: Ec. Geol., 38, 91-118. 29. MUGGE, O., (1892), Ueber den Kristallbau der pyrogenen quarz: Neues Jahrb. f. M.,P,, P., I, 1-14. 30. _____, (1907), Ueber die Zustand sänderung des Quarzes bei 570º: Neues Jahrb. f. M., P., P., Festband, 181-196. 31, _____, (1921), Quarz als geologisches Thermometer und die Bedeutung der Zu sammensetzungsflächen von Kristallzwillingen; Centrl. Min., Geol., 609-615; 641-648. 32. NEWHOUSE, W. H., (1933), The temperature of formation of the Mississippi Valley lead-zinc deposits: Ec. Geol., 28, 744-750. 33. _____, (1941), The direction of flow of mineralizing solutions: Ec. Geol.,36, 612-630, 34. PARRISH, WILLIAM, AND GoRDoN, S. G., (1945), Orientation techniques for the manufacture of quartz oscillator-plates: Am. Mineral., 30, 296-325. 35. SAPAROVA, JISKRA, (1938), Quartz from Wermsdorff in northern Moravia: Casopos Zemskeho Musea v. Brise, 30, 32 pp. 36. STOIBER, RICHARD E., TOLMAN, CARL, AND BUTLER, ROBERT D., (1945), Geology of quartz crystal deposits; Am. Mineral., 30, 245-269. 37. THOMAS, L. A., (1945), Terminology of interpenetrating twins in low-quartz: Nature, 155, 424, (April 7). 38. THOMPSON, M. R., (1937), How to tell right-handed from left-handed quartz crystals: Rocks and Minerals, 12, 38-43. 39. TROMMSDORF, WOLF, (1937), Das Verhältnis der Anzahl der Linksquarze zu der Rechtsquarze in einer grösseren Menge von Quarzkristallen: Neues. Jahrb. f. M., P., P., ß. B., Abt. A, 462 495. 40. TUTTON, A. E. H., (1922), Crystallography and Practical Crystal Measurement, vol. 1, Form and Structure, MacMillan. 41. TWENHOFEL, W. S., (1947), The temperature of crystallization of a fluorite crystal from Luna County, New Mexico: Ec. Geol., 42, 78-82. 42. VIROVLVANSKY, G. M., (1938a), Quartz as a geologic thermometer: Soc. Russe Miner, Mem. 67, Iv. 2, 236-246. 43. (1938b), On the question about the mirogenetic importance of vicinal figures on the edges of quartz: Soc. Russe Miner., Mem.,., 67, Iv. 2, 446-450. 44. WILLARD, G. W., (1944), Use of the etch technique for determining orientation and twinning in quartz crystals: Bell Sys. Tech. Jour., 23, 11-51. 45. WINCHELL, A. N., (1933), Elements of Optical Mineralogy, part II, John Wiley and and Sons, New York. 46. WRIGHT, F. E., AND LARSEN, E. S., (1909), Quartz as a geologic thermometer: Ana, Jour. Sci., 4th ser., 27, 421-447. 47. ZINSERLING, E. V., (1941), Quartz twinning control under alpha-beta inversion; Quartz coloring as dependent on its twinning capacity under alpha-beta conversion; (and Laemmlein, G. G.) Conversion of a negative quartz rhombohedron into a positive one as a result: of alpha-beta transformation: Comple Rendu, Acad. Sci., U.S.S.R., 33, 365 368, 419. 48. ZIRKEL, F., (1897), Elemente der Mineralogie (Naumann), Leipzig. NOTES 1 Published by permission of the Director, U. S. Geological Survey. 2 The term low-quartz refers, in this paper, to low-temperature quartz, that modification of ten called alpha and occasionally called beta which is stable below 573° C. 3 Symposium on quartz oscillator-plates, Am. Mineral., 30, 205-468, nos. 5 and 6 (1945); also other numbers of the Am. Mineral.; see also Bell System Tech. Jour.; reports and information circulars from the Office of the Chief Signal Officer, War Department; bulletins of the Fort Monmouth (Long Branch) Crystal Laboratories. 4 Personal communication 5 The writer is indebted to Mr. J. C. Wynn for the opportunity to study a set of 100 unpublished drawings of phantom crystals from Brazil. Johnston's and Butler's (1946) illustrations of phantoms are from this set. 6 The problem of asymmetry of apices and direction of flow of solutions does not enter into this discussion (Newhouse, 1941; Bandy, 1942; Engel, 1946). The Brazilian. crystals apparently have retained the asymmetry of the "seed" crystal of the phantoms throughout the growth of the phantoms.
|